题目内容
19.已知集合$A=\{x|y=\sqrt{x-1}\},A∩B=∅$,则集合B不可能是( )| A. | {x|4x<2x+1} | B. | $\left\{{y\left|{y=\sqrt{x-1}}\right.}\right\}$ | ||
| C. | $\{y|y=sinx,-\frac{π}{3}≤x≤\frac{π}{6}\}$ | D. | $\left\{{(x,y)\left|{y={{log}_2}(-{x^2}+2x+1)}\right.}\right\}$ |
分析 由已知得B?{x|x<1}或B不是数集,由此能求出结果.
解答 解:∵集合$A=\{x|y=\sqrt{x-1}\},A∩B=∅$,
∴A={x|x≥1},B?{x|x<1}或B不是数集,
在A中,{x|4x<2x+1}={x|x<1},故集合B可能是A;
在B中,{y|y=$\sqrt{x-1}≥0$},故不可能是B;
在C中,{y|y=sinx,-$\frac{π}{3}≤x≤\frac{π}{6}$}={y|-$\frac{\sqrt{3}}{2}≤y≤\frac{1}{2}$},故集合B可能是C;
在D中,{(x,y)|y=log2(-x2+2x+1)}是点集,与集合A没有公共元素,故集合B可能D.
故选:B.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集、子集定义的合理运用.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
9.在△ABC中,若$|\overrightarrow{AB}|=2$,$|\overrightarrow{AC}|=3$,$|\overrightarrow{BC}|=4$,O为△ABC的内心,且$\overrightarrow{AO}=λ\overrightarrow{AB}+μ\overrightarrow{BC}$,则λ+μ=( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{9}$ | C. | $\frac{7}{9}$ | D. | $\frac{5}{7}$ |
14.对于给定的直线l和平面a,在平面a内总存在直线m与直线l( )
| A. | 平行 | B. | 相交 | C. | 垂直 | D. | 异面 |
4.若函数$f(x)=\frac{d}{{a{x^2}-bx+c}}(a,b,c,d∈R)$的图象如图所示,则a:b:c:d=( )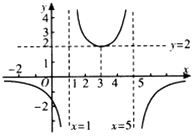

| A. | 1:6:5:(-8) | B. | 1:6:5:8 | C. | 1:(-6):5:8 | D. | 1:(-6):5:(-8) |
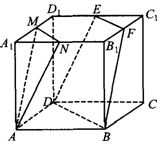 如图,已知棱长为4的正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1D1,A1B1,D1C1,B1C1的中点,求证:平面AMN∥平面EFBD.
如图,已知棱长为4的正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1D1,A1B1,D1C1,B1C1的中点,求证:平面AMN∥平面EFBD.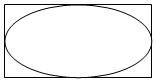 如图,矩形长为5,宽为3,在矩形内随机撒100颗黄豆,数得落在椭圆内的黄豆数为60颗,以此实验数据为依据可以估算椭圆的面积约为( )
如图,矩形长为5,宽为3,在矩形内随机撒100颗黄豆,数得落在椭圆内的黄豆数为60颗,以此实验数据为依据可以估算椭圆的面积约为( )