题目内容
14．对于给定的直线l和平面a，在平面a内总存在直线m与直线l（ ）| A． | 平行 | B． | 相交 | C． | 垂直 | D． | 异面 |
分析 本题可采用分类讨论，对答案进行排除，分别讨论直线l和平面α平行，直线l和平面α相交，直线l?平面α，三种情况，排除错误答案后，即可得到结论．
解答 解：若直线l和平面α平行，则平面α内的直线与l平行或异面，不可能相交，可排除答案A；
若直线l和平面α相交，则平面α内的直线与l相交或异面，不可能平行，可排除答案B；
若直线l?平面α，则平面α内的直线与l相交或平行，不可能异面，可排除答案D；
故选C．
点评 本题考查的知识点是空间中直线与直线之间的位置关系，其中熟练掌握直线与平面位置关系的几何特征，及直线与直线位置关系的结构特征是解答本题的关键．
练习册系列答案
53随堂测系列答案
相关题目
5．已知抛物线y2=2px的准线方程是x=-2，则p的值为（ ）
| A． | 2 | B． | 4 | C． | -2 | D． | -4 |
2．已知直线l的方向向量$\overrightarrow a=（1，1，0）$，平面α的一个法向量为$\overrightarrow n=（1，1，-\sqrt{6}）$，则直线l与平面α所成的角为（ ）
| A． | 120° | B． | 60° | C． | 30° | D． | 150° |
9．
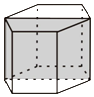如图，已知正六棱柱的最大对角面的面积为4m2，互相平行的两个侧面的距离为 2m，则这个六棱柱的体积为（ ）
如图，已知正六棱柱的最大对角面的面积为4m2，互相平行的两个侧面的距离为 2m，则这个六棱柱的体积为（ ）| A． | 3m3 | B． | 6m3 | C． | 12m3 | D． | 15m3 |
19．已知集合$A=\{x|y=\sqrt{x-1}\}，A∩B=∅$，则集合B不可能是（ ）
| A． | {x|4x＜2x+1} | B． | $\left\{{y\left|{y=\sqrt{x-1}}\right.}\right\}$ | ||
| C． | $\{y|y=sinx，-\frac{π}{3}≤x≤\frac{π}{6}\}$ | D． | $\left\{{（x，y）\left|{y={{log}_2}（-{x^2}+2x+1）}\right.}\right\}$ |
6．定义在区间（0，+∞）上的函数f（x）使不等式xf'（x）＜4f（x）恒成立，其中f'（x）为f（x）的导数，则（ ）
| A． | $\frac{f（2）}{f（1）}＜16$ | B． | $\frac{f（2）}{f（1）}＜8$ | C． | $\frac{f（2）}{f（1）}＜4$ | D． | $\frac{f（2）}{f（1）}＜2$ |
4．直线2x-y-3=0的倾斜角为θ，则tanθ=（ ）
| A． | $\frac{1}{2}$ | B． | $-\frac{1}{2}$ | C． | 2 | D． | -2 |