题目内容
10.已知椭圆长轴长为4,焦点 F1(-1,0),F2(1,0),求椭圆标准方程和离心率.分析 由题意可得2a,进一步得到a,由隐含条件求得b,则椭圆标准方程可求,再由离心率定义求得椭圆的离心率.
解答 解:由已知得2a=4,∴a=2,
又焦点 F1(-1,0),F2(1,0),∴c=1,
则b2=a2-c2=3,
∴椭圆的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
椭圆的离心率为e=$\frac{c}{a}=\frac{1}{2}$.
点评 本题考查椭圆的简单性质,考查了椭圆标准方程的求法,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知抛物线y2=2px的准线方程是x=-2,则p的值为( )
| A. | 2 | B. | 4 | C. | -2 | D. | -4 |
2.已知直线l的方向向量$\overrightarrow a=(1,1,0)$,平面α的一个法向量为$\overrightarrow n=(1,1,-\sqrt{6})$,则直线l与平面α所成的角为( )
| A. | 120° | B. | 60° | C. | 30° | D. | 150° |
19.已知集合$A=\{x|y=\sqrt{x-1}\},A∩B=∅$,则集合B不可能是( )
| A. | {x|4x<2x+1} | B. | $\left\{{y\left|{y=\sqrt{x-1}}\right.}\right\}$ | ||
| C. | $\{y|y=sinx,-\frac{π}{3}≤x≤\frac{π}{6}\}$ | D. | $\left\{{(x,y)\left|{y={{log}_2}(-{x^2}+2x+1)}\right.}\right\}$ |
20.已知P是抛物线y2=4x上一动点,则点P到直线l:2x-y+3=0和直线x=-2的距离之和的最小值是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}+1$ | C. | 2 | D. | $\sqrt{5}$-1 |

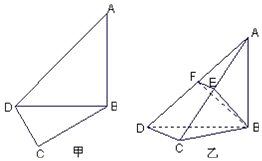 如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.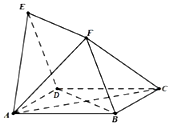 如图,平面四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
如图,平面四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.