题目内容
9.在空间直角坐标系中,已知$\overrightarrow{a}$=(2,2,-1),$\overrightarrow{b}$=(-1,3,1),则$\overrightarrow{a}$、$\overrightarrow{b}$夹角的余弦值是$\frac{\sqrt{11}}{11}$.分析 cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$,由此能求出$\overrightarrow{a}$、$\overrightarrow{b}$夹角的余弦值.
解答 解:∵$\overrightarrow{a}$=(2,2,-1),$\overrightarrow{b}$=(-1,3,1),
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{-2+6-1}{\sqrt{9}•\sqrt{11}}$=$\frac{\sqrt{11}}{11}$.
∴$\overrightarrow{a}$、$\overrightarrow{b}$夹角的余弦值是$\frac{\sqrt{11}}{11}$.
故答案为:$\frac{{\sqrt{11}}}{11}$.
点评 本题考查空间向量的夹角的余弦值的求法,是基础题,解题时要认真审题,注意向量夹角余弦公式的合理运用.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
19.已知集合$A=\{x|y=\sqrt{x-1}\},A∩B=∅$,则集合B不可能是( )
| A. | {x|4x<2x+1} | B. | $\left\{{y\left|{y=\sqrt{x-1}}\right.}\right\}$ | ||
| C. | $\{y|y=sinx,-\frac{π}{3}≤x≤\frac{π}{6}\}$ | D. | $\left\{{(x,y)\left|{y={{log}_2}(-{x^2}+2x+1)}\right.}\right\}$ |
20.已知P是抛物线y2=4x上一动点,则点P到直线l:2x-y+3=0和直线x=-2的距离之和的最小值是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}+1$ | C. | 2 | D. | $\sqrt{5}$-1 |
4.直线2x-y-3=0的倾斜角为θ,则tanθ=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 2 | D. | -2 |
13.在空间直角坐标系中,一定点到三个坐标平面的距离都是2,那么该定点到原点的距离是( )
| A. | $\sqrt{6}$ | B. | $2\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{2\sqrt{6}}}{3}$ |
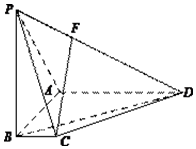 如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.
如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.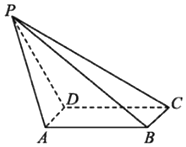 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AD⊥PD,BC=1,PC=2$\sqrt{3}$,PD=CD=2,则二面角A-PB-C的正切值为$\frac{\sqrt{15}}{9}$.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AD⊥PD,BC=1,PC=2$\sqrt{3}$,PD=CD=2,则二面角A-PB-C的正切值为$\frac{\sqrt{15}}{9}$.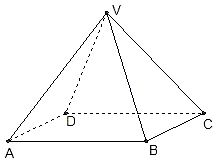 如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它侧面都是侧棱长为$\sqrt{5}$的等腰三角形,试画出二面角V-AB-C的平面角,并求出它的度数.
如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它侧面都是侧棱长为$\sqrt{5}$的等腰三角形,试画出二面角V-AB-C的平面角,并求出它的度数.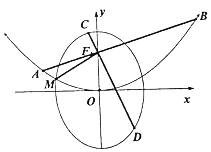 已知F1为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1的上焦点,F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.
已知F1为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1的上焦点,F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.