题目内容
4.若函数$f(x)=\frac{d}{{a{x^2}-bx+c}}(a,b,c,d∈R)$的图象如图所示,则a:b:c:d=( )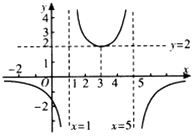
| A. | 1:6:5:(-8) | B. | 1:6:5:8 | C. | 1:(-6):5:8 | D. | 1:(-6):5:(-8) |
分析 根据图象可先判断出分母的表达式的零点,然后利用特殊点关系式即可.
解答 解:由图象可知x≠1,5,
∴分母上必定可分解为k(x-1)(x-5)=ax2-bx+c,可得a=k,b=6k,c=5k,
∵在x=3时有y=2,即2=$\frac{d}{9a-3b+c}$,
∴d=-8k
∴a:b:c:d=1:6:5:(-8),
故选:A.
点评 本题考查了利用图象信息推导所给函数的系数和常数部分.考查分析问题解决问题的能力.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
19.已知集合$A=\{x|y=\sqrt{x-1}\},A∩B=∅$,则集合B不可能是( )
| A. | {x|4x<2x+1} | B. | $\left\{{y\left|{y=\sqrt{x-1}}\right.}\right\}$ | ||
| C. | $\{y|y=sinx,-\frac{π}{3}≤x≤\frac{π}{6}\}$ | D. | $\left\{{(x,y)\left|{y={{log}_2}(-{x^2}+2x+1)}\right.}\right\}$ |
16.定义在R上的函数f(x)在(6,+∞)上为增函数,且函数y=f(x+6)为偶函数,则( )
| A. | f(4)<f(7) | B. | f(4)>f(7) | C. | f(5)>f(7) | D. | f(5)<f(7) |
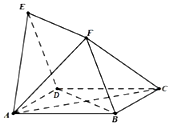 如图,平面四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
如图,平面四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.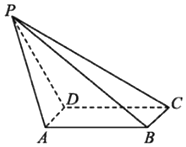 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AD⊥PD,BC=1,PC=2$\sqrt{3}$,PD=CD=2,则二面角A-PB-C的正切值为$\frac{\sqrt{15}}{9}$.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AD⊥PD,BC=1,PC=2$\sqrt{3}$,PD=CD=2,则二面角A-PB-C的正切值为$\frac{\sqrt{15}}{9}$.