题目内容
11.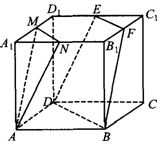 如图,已知棱长为4的正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1D1,A1B1,D1C1,B1C1的中点,求证:平面AMN∥平面EFBD.
如图,已知棱长为4的正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1D1,A1B1,D1C1,B1C1的中点,求证:平面AMN∥平面EFBD.
分析 证法一:设正方体的棱长为4,如图建立空间直角坐标系,利用向量法,可证得:MN∥平面EFBD,AK∥平面EFBD,进而得到平面AMN∥平面EFBD.
证法二:求出平面AMN的法向量和平面EFBD的法向量,根据两个法向量平行,可得平面AMN∥平面EFBD.
解答  (本小题满分13分)
(本小题满分13分)
证法一:设正方体的棱长为4,如图建立空间直角坐标系,
则D(0,0,0),A(4,0,0),M(2,0,4),
N(4,2,4),B(4,4,0),E(0,2,4),F(2,4,4).
取MN的中点K,EF的中点G,BD的中点O,则O(2,2,0),K(3,1,4),G(1,3,4).
$\overrightarrow{MN}$=(2,2,0),$\overrightarrow{EF}$=(2,2,0),$\overrightarrow{AK}$=(-1,1,4),$\overrightarrow{OG}$=(-1,1,4),
∴$\overrightarrow{MN}$∥$\overrightarrow{EF}$,$\overrightarrow{AK}=\overrightarrow{OG}$,
∴MN∥EF,AK∥OG,
∴MN∥平面EFBD,AK∥平面EFBD,
∴平面AMN∥平面EFBD.
证法二:设平面AMN的法向量是$\overrightarrow{a}$=(a1,a2,a3),平面EFBD的法向量是$\overrightarrow{b}$=(b1,b2,b3).
由$\overrightarrow{a}•\overrightarrow{AM}=0,\overrightarrow{a}•\overrightarrow{AN}=0$,
得$\left\{{\begin{array}{l}-2{a_1}+4{a_3}=0\\ 2{a_2}+4{a_3}=0\end{array}}\right.$取a3=1,得$\overrightarrow{a}$=(2,-2,1).
由${\vec b}•\overrightarrow{DE}=0,{\vec b}•\overrightarrow{BF}=0$,
得$\left\{{\begin{array}{l}2{b_2}+4{b_3}=0\\-2{b_1}+4{b_3}=0\end{array}}\right.$取b3=1,得$\overrightarrow{b}$=(2,-2,1).
∵$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴平面AMN∥平面EFBD.
点评 本题考查的知识点是平面与平面平行的判断,利用向量证明面面平行,难度中档.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案| A. | 120° | B. | 60° | C. | 30° | D. | 150° |
| A. | {x|4x<2x+1} | B. | $\left\{{y\left|{y=\sqrt{x-1}}\right.}\right\}$ | ||
| C. | $\{y|y=sinx,-\frac{π}{3}≤x≤\frac{π}{6}\}$ | D. | $\left\{{(x,y)\left|{y={{log}_2}(-{x^2}+2x+1)}\right.}\right\}$ |
| A. | $\frac{f(2)}{f(1)}<16$ | B. | $\frac{f(2)}{f(1)}<8$ | C. | $\frac{f(2)}{f(1)}<4$ | D. | $\frac{f(2)}{f(1)}<2$ |
| A. | f(4)<f(7) | B. | f(4)>f(7) | C. | f(5)>f(7) | D. | f(5)<f(7) |
| A. | $\sqrt{3}$ | B. | $\sqrt{5}+1$ | C. | 2 | D. | $\sqrt{5}$-1 |

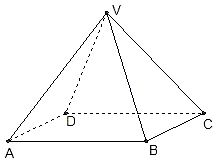 如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它侧面都是侧棱长为$\sqrt{5}$的等腰三角形,试画出二面角V-AB-C的平面角,并求出它的度数.
如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它侧面都是侧棱长为$\sqrt{5}$的等腰三角形,试画出二面角V-AB-C的平面角,并求出它的度数.