题目内容
7.设全集U={-2,-1,1,2,3},A={-2,1}.B={x|(x+1)(mx-4)=0}(m∈R).(1)当m=2时,求∁u(A∪B);
(1)若A∩B≠∅,求m的值.
分析 (1)当m=2时,B={-1,2},从而求得A∪B={-2,-1,2};故∁u(A∪B)={1,3};
(2)由题意知-2∈B或1∈B,从而可得-2m-4=0或m-4=0.
解答 解:(1)当m=2时,B={x|(x+1)(2x-4)=0}={-1,2},
故A∪B={-2,-1,2};
故∁u(A∪B)={1,3};
(2)∵A∩B≠∅,
∴-2∈B或1∈B,
故-2m-4=0或m-4=0,
故m=-2或m=4.
点评 本题考查了集合的化简与运算的应用.

练习册系列答案
相关题目
18.设x,y满足约束条件$\left\{\begin{array}{l}{x-3y+4≥0,}&{\;}\\{x+2y-1≥0,}&{\;}\\{3x+y-8≤0.}&{\;}\end{array}\right.$,则z=2x-y的最小值与最大值分别为( )
| A. | -3与7 | B. | 2与3 | C. | 2与7 | D. | 3与7 |
19.过原点且倾斜角为30°的直线l被圆C:x2+y2+4y-3=0所截得的弦长为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
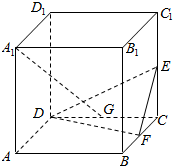 如图,正方体ABCD-A1B1C1D1中,E,F,G分别是棱CC1,BC,CD的中点,求证:A1G⊥平面DEF.
如图,正方体ABCD-A1B1C1D1中,E,F,G分别是棱CC1,BC,CD的中点,求证:A1G⊥平面DEF.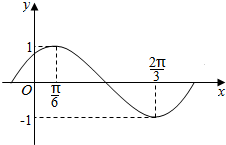 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.