题目内容
2.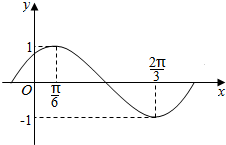 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.(1)求f(x)的最小正周期及解析式;
(2)求不等式f(x)>$\frac{1}{2}$的解集.
分析 (1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(2)由题意可得 sin(2x+$\frac{π}{6}$)>$\frac{1}{2}$,故有 2kπ+$\frac{π}{6}$<2x+$\frac{π}{6}$<2kπ+$\frac{5π}{6}$,k∈Z,由此求得x的范围.
解答 解:(1)由函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象,
可得A=1,$\frac{2π}{3}$-$\frac{π}{6}$=$\frac{1}{2}•\frac{2π}{ω}$,求得ω=2.
再根据五点法作图可得2×$\frac{π}{6}$+φ=$\frac{π}{2}$,求得φ=$\frac{π}{6}$,故函数f(x)=sin(2x+$\frac{π}{6}$),可得它的周期为$\frac{2π}{2}$=π.
(2)由不等式f(x)>$\frac{1}{2}$ 可得 sin(2x+$\frac{π}{6}$)>$\frac{1}{2}$,可得 2kπ+$\frac{π}{6}$<2x+$\frac{π}{6}$<2kπ+$\frac{5π}{6}$,k∈Z,
求得kπ<x<kπ+$\frac{π}{3}$,故 sin(2x+$\frac{π}{6}$)>$\frac{1}{2}$的解集为{x|kπ<x<kπ+$\frac{π}{3}$,k∈Z}.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,解三角不等式,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知直线x+4y=2与x轴,y轴分别交于A,B两点,若动点P(a,b)在线段AB上,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为( )
| A. | $\frac{7}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
10.设奇函数f(x)在(0,+∞)上为减函数,且f(1)=0,则不等式$\frac{2f(x)-f(x)}{3x}$<0的解集为( )
| A. | (-1,0)∪(1,+∞) | B. | (-∞,-1)∪(0,1) | C. | (-∞,-1)∪(1,+∞) | D. | (-1,0)∪(0,1) |
14.函数f(x)的定义域为[-4,2),则f(2x)的定义域为( )
| A. | -8≤x<4 | B. | -2≤x<4 | C. | -4≤x<2 | D. | -2≤x<1 |
11.已知偶函数f(x)的定义域为[-10,10],当x≥0时,f(x)=$\left\{\begin{array}{l}{\sqrt{4{-x}^{2}}}&{x∈[0,2]}\\{\sqrt{4{-(x-4)}^{2}}}&{x∈[2,6]}\\{\sqrt{4{-(x-8)}^{2}}}&{x∈[6,10]}\end{array}\right.$,若关于x的方程f(x)-kx=0有且只有三个不同的实数根,则实数k的取值范围是( )
| A. | (-$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{15}}{15}$) | B. | ($\frac{\sqrt{15}}{15}$,$\frac{\sqrt{3}}{3}$) | ||
| C. | (-$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{15}}{15}$)∪($\frac{\sqrt{15}}{15}$,$\frac{\sqrt{3}}{3}$) | D. | (-$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{15}}{15}$]∪[$\frac{\sqrt{15}}{15}$,$\frac{\sqrt{3}}{3}$) |