题目内容
 如图,四边形ABCD中,AB=2,C=2
如图,四边形ABCD中,AB=2,C=2| 2 |
(1)求∠BAC;
(2)求边AD的长.
考点:解三角形的实际应用
专题:综合题,解三角形
分析:(1)连接AC,在三角形ABC中,由AB,BC及cosB的值,利用余弦定理求出AC的长,利用勾股定理的逆定理得到三角形ABC为等腰直角三角形,进而求出∠BAC、∠ACD的度数;
(2)由AC,CD,利用余弦定理即可求出AD的长.
(2)由AC,CD,利用余弦定理即可求出AD的长.
解答:
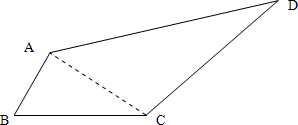 解:(1)连接AC,
解:(1)连接AC,
∵AB=2,BC=2
,∠B=45°,
∴由余弦定理得:AC2=4+8-8=4,
解得:AC=2,
∴∠BAC=90°;
(2)在△ACD中,AC=2,CD=7,∠ACD=60°,
由余弦定理AD2=AC2+CD2-2AC×CD×cos∠ACD,得AD2=4+49-2×2×7×cos60°=39,
则AD=
.
 解:(1)连接AC,
解:(1)连接AC,∵AB=2,BC=2
| 2 |
∴由余弦定理得:AC2=4+8-8=4,
解得:AC=2,
∴∠BAC=90°;
(2)在△ACD中,AC=2,CD=7,∠ACD=60°,
由余弦定理AD2=AC2+CD2-2AC×CD×cos∠ACD,得AD2=4+49-2×2×7×cos60°=39,
则AD=
| 39 |
点评:此题考查了余弦定理,勾股定理的逆定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
已知f(x)=lnx,则f(x)的导数为f′(x),则f′(1)的值为( )
| A、e | B、0 | C、1 | D、ln2 |
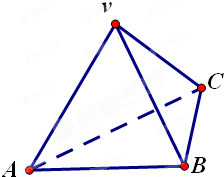 如图,在三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2
如图,在三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2