题目内容
若函数f(x)的定义域和值域均为区间G,则称区间G为函数f(x)的“管控区间”.
(1)求函数f(x)=x2-2x形如[a,+∞)(a∈R)的“管控区间”;
(2)函数g(x)=|1-
|(x>0)是否存在形如[a,b]的“管控区间”,若存在,求出实数a、b的值,若不存在,请说明理由.
(1)求函数f(x)=x2-2x形如[a,+∞)(a∈R)的“管控区间”;
(2)函数g(x)=|1-
| 1 |
| x |
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)根据“管控区间的概念求解即可;
(2)分类讨论函数的单调性,使其满足函数有”管控区间,列方程解方程即可.
(2)分类讨论函数的单调性,使其满足函数有”管控区间,列方程解方程即可.
解答:
解:(1)∵f(x)=x2─2x=(x─1)2─1,∴f(x)的值域为[─1,+∞).
故[─1,+∞)是函数f (x)的一个“管控区间”.
又函数f(x)的图象与y=x有一个交点(3,3),∴[3,+∞)也是函数f(x)的一个“管控区间”.
综上,函数f(x)有两个形如[a,+∞)的“管控区间”[─1,+∞)和[3,+∞)…(6分)
(2)若存在实数a、b使得函数g(x)=|1─
|(x>0)有形如[a,b]的“管控区间”,则a>0.
∵g(x)=|1─
|=
.
∴①当a,b∈(0,1)时,g(x)=
─1在(0,1)上为减函数.
故
⇒
⇒a=b,与a<b矛盾.
②当a,b∈[1,+∞)时,g(x)=1─
在[1,+∞)上为增函数.
故
即
,
又a,b是x2-x+1=0的根,但次方程无解,
故不存在满足条件的实数a,b.
③当a∈(0,1),b∈[1,+∞)时,由于1∈[a,b],而g(1)=0,
综上,不存在满足条件的实数a,b.
故[─1,+∞)是函数f (x)的一个“管控区间”.
又函数f(x)的图象与y=x有一个交点(3,3),∴[3,+∞)也是函数f(x)的一个“管控区间”.
综上,函数f(x)有两个形如[a,+∞)的“管控区间”[─1,+∞)和[3,+∞)…(6分)
(2)若存在实数a、b使得函数g(x)=|1─
| 1 |
| x |
∵g(x)=|1─
| 1 |
| x |
|
∴①当a,b∈(0,1)时,g(x)=
| 1 |
| x |
故
|
|
②当a,b∈[1,+∞)时,g(x)=1─
| 1 |
| x |
故
|
|
又a,b是x2-x+1=0的根,但次方程无解,
故不存在满足条件的实数a,b.
③当a∈(0,1),b∈[1,+∞)时,由于1∈[a,b],而g(1)=0,
综上,不存在满足条件的实数a,b.
点评:考查学生求函数定义域、值域的能力,以及利用导数研究函数增减性的能力.

练习册系列答案
相关题目
已知函数f(x)满足:f(m+n)=f(m)f(n),f(1)=3,则
+
+
+
的值等于( )
| f2(1)+f(2) |
| f(1) |
| f2(2)+f(4) |
| f(3) |
| f2(3)+f(6) |
| f(5) |
| f2(4)+f(8) |
| f(7) |
| A、36 | B、24 | C、18 | D、12 |
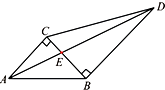 如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.若记
如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.若记