题目内容
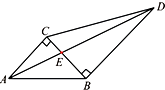 如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.若记
如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.若记| AB |
| a |
| AC |
| b |
| a |
| b |
| CD |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:利用向量共线定理可得
=
,再利用向量三角形法则即可得出.
| BD |
| 3 |
| AC |
解答:
解:(1)∵AC⊥BC,BD⊥BC,
∴BD∥AC,
∵|
|=
|
|=
|
|,
∴
=
,
∴
=
+
=
+
,
∴
=
+
=-
+
+
=
+(
-1)
.
故答案为
+(
-1)
.
∴BD∥AC,
∵|
| BD |
| 3 |
| BC |
| 3 |
| AC |
∴
| BD |
| 3 |
| AC |
∴
| AD |
| AB |
| BD |
| a |
| 3 |
| b |
∴
| CD |
| CA |
| AD |
| b |
| a |
| 3 |
| b |
| a |
| 3 |
| b |
故答案为
| a |
| 3 |
| b |
点评:本题考查了向量共线定理、数量积运算及其性质,属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 (理科)如图,边长为2的正方形ABCD和正方形ABEF所在的面所成角为60°,M和N分别是AC和BF上的点,且AM=FN,求线段MN长的取值范围( )
(理科)如图,边长为2的正方形ABCD和正方形ABEF所在的面所成角为60°,M和N分别是AC和BF上的点,且AM=FN,求线段MN长的取值范围( )| A、[0.5,2] | ||
| B、[1.5,2] | ||
C、[
| ||
| D、[1,2] |
已知为f(x)奇函数,在[3,6]上是增函数,[3,6]上的最大值为8,最小值为-1,则2f(-6)+f(-3)等于( )
| A、-15 | B、-13 | C、-5 | D、5 |
函数f(x)=lnx+
-1的零点个数为( )
| 1 |
| x |
| A、0 | B、1 | C、2 | D、3 |
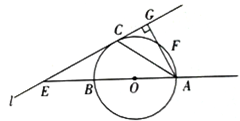 已知:直线AB过圆心O,交⊙O于A、B,直线AF交⊙O于A、F(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
已知:直线AB过圆心O,交⊙O于A、B,直线AF交⊙O于A、F(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.