题目内容
已知函数f（x）=
，则其定义域为（ ）
| ||
| |x|-1 |
| A、[-2，2] |
| B、[-2，1）∪（1，2] |
| C、[-2，-1）∪（-1，1）∪（1，2] |
| D、（-2，-1）∪（-1，1）∪（1，2） |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数f（x）的解析式，列出不等式组
，求出解集即可．
|
解答：
解：∵函数f（x）=
，
∴
；
解得-2≤x≤2，且x≠±1；
∴f（x）定义域为[-2，-1）∪（-1，1）∪（1，2]．
故选：C．
| ||
| |x|-1 |
∴
|
解得-2≤x≤2，且x≠±1；
∴f（x）定义域为[-2，-1）∪（-1，1）∪（1，2]．
故选：C．
点评：本题考查了利用函数的解析式，求函数定义域的问题，解题的关键是列出使函数解析式有意义的不等式组，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
函数y=x3+
是（ ）
| 1 |
| x |
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |
函数f（x）=log2|x-1|的图象大致是（ ）
A、 |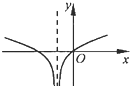
B、 |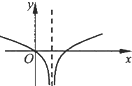
C、 |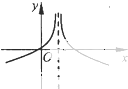
D、 |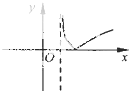
已知命题p：π是有理数，q：-π是负数，给出下列四个复合命题：①p或q，②p且q，③非p，④非q，其中真命题是（ ）
| A、①，② | B、①，③ |
| C、②，③ | D、②，④ |
“a=-2”是“直线a2x+2y+1=0与直线x+ay-2=0互相垂直”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |