题目内容
已知函数f(x)是奇函数,且f(x+2)=-f(x),若f(x)在[-1,0]上是增函数,f(1),f(
),f(
)的大小关系是( )
| 3 |
| 2 |
| 13 |
| 3 |
A、f(1)<f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|
考点:函数的周期性,奇偶性与单调性的综合
专题:函数的性质及应用
分析:由f(x+2)=-f(x),得f(x+4)=f(x),利用函数奇偶性单调性之间的关系,即可比较大小.
解答:
解:∵f(x+2)=-f(x),函数f(x)是奇函数,
∴f(x+2)=-f(x)=f(-x),
∴函数f(x)关于x=1对称,
且f(x+4)=f(x),
∴函数是周期为4的周期数列.
∵f(x)在[-1,0]上是增函数,
∴f(x)在[-1,1]上是增函数,f(x)在[1,2]上是减函数,
f(
)=f(4+
)=f(
)=f(
),
∵f(x)在[1,2]上是减函数,且1<
<
,
∴f(1)>f(
)>f(
),
即f(
)<f(
)<f(1),
故选:D.
∴f(x+2)=-f(x)=f(-x),
∴函数f(x)关于x=1对称,
且f(x+4)=f(x),
∴函数是周期为4的周期数列.
∵f(x)在[-1,0]上是增函数,
∴f(x)在[-1,1]上是增函数,f(x)在[1,2]上是减函数,
f(
| 13 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
∵f(x)在[1,2]上是减函数,且1<
| 3 |
| 2 |
| 5 |
| 3 |
∴f(1)>f(
| 3 |
| 2 |
| 5 |
| 3 |
即f(
| 13 |
| 3 |
| 3 |
| 2 |
故选:D.
点评:本题主要考查函数值的大小比较,利用函数的奇偶性,对称性和单调性是解决本题的关键,综合考查函数的性质,考查学生的转化意识.

练习册系列答案
相关题目
若命题p:函数y=lg(1-x)的值域为R;命题q:函数y=2cosx是偶函数,且是R上的周期函数,则下列命题中为真命题的是( )
| A、p∧q |
| B、(¬p)∨(¬q) |
| C、(¬p)∧q |
| D、p∧(¬q) |
下列说法一定正确的是( )
| A、直角三角形绕其一边旋转形成圆锥 |
| B、等边三角形绕其一边旋转形成圆锥 |
| C、平面截圆锥所得的图形是圆 |
| D、过圆锥顶点的截面图形是等腰三角形 |
给出下列说法:
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②用相关指数可以刻画回归的效果,值越小说明模型的拟合效果越好;
③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型拟合效果越好.
其中正确的是( )
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②用相关指数可以刻画回归的效果,值越小说明模型的拟合效果越好;
③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型拟合效果越好.
其中正确的是( )
| A、①② | B、②③ | C、①③ | D、①②③ |
已知条件p:α是两条直线的夹角,条件q:α是第一象限的角.则“条件p”是“条件q”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
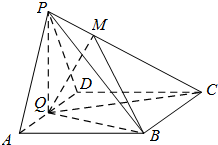 如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,平面PAD⊥平面ABCD,PA=PD=AD=2,Q为AD的中点,M是棱PC上一点,且PM=
如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,平面PAD⊥平面ABCD,PA=PD=AD=2,Q为AD的中点,M是棱PC上一点,且PM=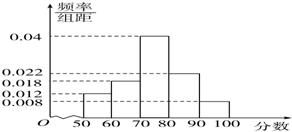 某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图.
某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图.