题目内容
若命题p:函数y=lg(1-x)的值域为R;命题q:函数y=2cosx是偶函数,且是R上的周期函数,则下列命题中为真命题的是( )
| A、p∧q |
| B、(¬p)∨(¬q) |
| C、(¬p)∧q |
| D、p∧(¬q) |
考点:复合命题的真假
专题:简易逻辑
分析:首先,分别判断命题p和命题q的真假,然后,结合复合命题的真值表进行判断即可.
解答:
解:由命题p:
∵1-x>0,
∴x<1,
∴函数y=lg(1-x)的值域为R,
∴命题p为真命题;
由命题q:
设函数y=f(x)=2cosx
则 f(-x)=2cos(-x)=2cosx=f(x),
∴f(-x)=f(x),
∴函数y=2cosx是偶函数,
∵f(x+2π)=2cos(x+2π)=2cosx=f(x),
∴函数y=2cosx是最小正周期为2π的函数,
∴命题q为真命题.
∴命题p∧q为真命题,
故选A.
∵1-x>0,
∴x<1,
∴函数y=lg(1-x)的值域为R,
∴命题p为真命题;
由命题q:
设函数y=f(x)=2cosx
则 f(-x)=2cos(-x)=2cosx=f(x),
∴f(-x)=f(x),
∴函数y=2cosx是偶函数,
∵f(x+2π)=2cos(x+2π)=2cosx=f(x),
∴函数y=2cosx是最小正周期为2π的函数,
∴命题q为真命题.
∴命题p∧q为真命题,
故选A.
点评:本题重点考查了复合命题的真假判断方法,理解逻辑联结词“且”、“或”是关键,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
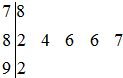 如图是2010年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为( )
如图是2010年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为( )| A、4.84 | B、0.8 |
| C、1.6 | D、3.2 |
若一元二次不等式f(x)>0的解集为{x|-2<x<1},则f(2x)<0的解集为( )
| A、{x|x<-2或x>0} |
| B、{x|x<0或x>2} |
| C、{x|x>0} |
| D、{x|x<0} |
已知点M(x1,y1)、N(x2,y2)的坐标满足不等式组
,若
=(1,-1),则
•
的取值范围是( )
|
| a |
| MN |
| a |
| A、[-3,3] |
| B、[-4,4] |
| C、[-6,6] |
| D、[-7,7] |
已知函数f(x)=x+
,若对任意x∈N*,都有f(x)≥f(3),则实数c的取值范围是( )
| c |
| x |
| A、[3,+∞) |
| B、{9} |
| C、[3,9] |
| D、[6,12] |
若复数z满足(z+2)i=5+5i(i为虚数单位),则z为( )
| A、3+5i | B、3-5i |
| C、-3+5i | D、-3-5i |
将51转化为二进制数得( )
| A、100111(2) |
| B、110011(2) |
| C、110110(2) |
| D、110101(2) |
已知函数f(x)是奇函数,且f(x+2)=-f(x),若f(x)在[-1,0]上是增函数,f(1),f(
),f(
)的大小关系是( )
| 3 |
| 2 |
| 13 |
| 3 |
A、f(1)<f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|