题目内容
若复数|z-3i|=5，求|z+2|的最大值和最小值．
考点：复数的代数表示法及其几何意义,复数求模
专题：数系的扩充和复数
分析：利用圆的复数形式的方程和复数形式的两点间的距离公式即可得出．
解答：
解：如图，满足|z-3i|=5的复数z所对应的点是以C（0，3）为圆心，5为半径的圆．
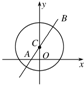|z+2|表示复数z所对应的点Z和点A（-2，0）的距离，由题设z所对应的点在圆周上，而此圆周上的点到点A距离的最大值与最小值是过A的圆周的直径被A点所分成的两部分．
∴|AC|=
=
．
∴|z+2|max=5+
，|z+2|min=5-
．
|z+2|表示复数z所对应的点Z和点A（-2，0）的距离，由题设z所对应的点在圆周上，而此圆周上的点到点A距离的最大值与最小值是过A的圆周的直径被A点所分成的两部分．∴|AC|=
| (-2)2+32 |
| 13 |
∴|z+2|max=5+
| 13 |
| 13 |
点评：本题考查了圆的复数形式的方程和复数形式的两点间的距离公式及其点与圆上的点的距离，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
已知函数f(x)=x+
，若对任意x∈N*，都有f（x）≥f（3），则实数c的取值范围是（ ）
| c |
| x |
| A、[3，+∞） |
| B、{9} |
| C、[3，9] |
| D、[6，12] |
若（
-x
）n展开式中含有x2项，则n的最小值是（ ）
| 1 |
| x |
| x |
| A、15 | B、8 | C、7 | D、3 |
i是虚数单位，复数
=（ ）
| i(2+i) |
| 1-2i |
| A、i | B、-i | C、1 | D、-1 |
已知函数f（x）是奇函数，且f（x+2）=-f（x），若f（x）在[-1，0]上是增函数，f(1)，f(
)，f(
)的大小关系是（ ）
| 3 |
| 2 |
| 13 |
| 3 |
A、f(1)＜f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|
