题目内容
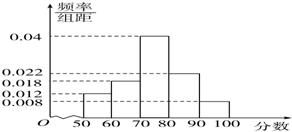 某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图.
某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图.(1)估计全市学生综合素质成绩的平均值;
(2)若评定成绩不低于80分为优秀,视频率为概率,从全市学生中任取3名学生(看作有放回的抽样),变量ξ表示3名学生中成绩优秀的人数,求变量ξ的分布列及期望E(ξ).
考点:离散型随机变量的期望与方差,众数、中位数、平均数
专题:综合题,概率与统计
分析:(1)求每个小矩形底边中点的横坐标乘以对应小矩形的面积之和,可得数据的平均数;
(2)由题意,优秀的概率为0.3,不优秀的概率为0.7,ξ的可能取值为0,1,2,3,求出相应的概率,即可求出分布列与期望.
(2)由题意,优秀的概率为0.3,不优秀的概率为0.7,ξ的可能取值为0,1,2,3,求出相应的概率,即可求出分布列与期望.
解答:
解:(1)平均数
=55×0.012×10+65×0.018×10+75×0.04×10+85×0.022×10+95×0.08×10
=74.6,
∴学生综合素质成绩的平均值为74.6;
(2)由题意,优秀的概率为0.3,不优秀的概率为0.7,ξ的可能取值为0,1,2,3,则
P(ξ=0)=0.73=0.343,P(ξ=1)=
•0.3•0.72=0.441,
P(ξ=2)=
•0.32•0.7=0.189,P(ξ=3)=0.33=0.027,
∴ξ的分布列为
E(ξ)=1×0.441+2×0.189+3×0.027=0.901.
. |
| x |
=74.6,
∴学生综合素质成绩的平均值为74.6;
(2)由题意,优秀的概率为0.3,不优秀的概率为0.7,ξ的可能取值为0,1,2,3,则
P(ξ=0)=0.73=0.343,P(ξ=1)=
| C | 1 3 |
P(ξ=2)=
| C | 2 3 |
∴ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | 0.343 | 0.441 | 0.189 | 0.027 |
点评:本题考查了频率分布直方图,考查了分布列与期望,解题的关键是确定变量的取值,求出相应的概率.

练习册系列答案
相关题目
将51转化为二进制数得( )
| A、100111(2) |
| B、110011(2) |
| C、110110(2) |
| D、110101(2) |
已知函数f(x)是奇函数,且f(x+2)=-f(x),若f(x)在[-1,0]上是增函数,f(1),f(
),f(
)的大小关系是( )
| 3 |
| 2 |
| 13 |
| 3 |
A、f(1)<f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|