题目内容
我们把一系列向量ai(i=1,2,3,…n)按次序排成一列,称之为向量列,记作{
}.已知非零的向量列满足:
=(x1,y1),
=(xn,yn)=
(xn-1-yn-1,xn-1+yn-1)(n≥2).
(1)证明数列{|
|}是等比数列;
(2)设θn表示向量
,
的夹角的弧度数(n≥2),若bn=
,Sn=b2+b3+…+bn,求Sn;
(3)设
=(1,2),把
,
,…,
中所有与
共线的向量按原来的顺序排成一列,记为
,
,…,
,…,令
=
+
+…+
,O为坐标原点,求点列{Dn}的极限点D的坐标.(注:若点Dn坐标为(tn,vn),
tn=t,
vn=v,则点D(t,v)为点列{Dn}的极限点.
| an |
| a1 |
| an |
| 1 |
| 2 |
(1)证明数列{|
| an |
(2)设θn表示向量
| an-1 |
| an |
| π |
| 4n(n-1)θn |
(3)设
| a1 |
| a1 |
| a2 |
| an |
| a1 |
| d1 |
| d2 |
| dn |
| ODn |
| d1 |
| d2 |
| dn |
| lim |
| n→∞ |
| lim |
| n→∞ |
考点:数列与向量的综合,数列的极限
专题:等差数列与等比数列
分析:(1)得出|
|≠0,
=
,运用等比数列的定义判断,(2)化简得出bn=
=
=
-
,裂项求解,(3)根据向量的平行得出tn=
=
[1-(-
)n],vn=2×
=
[1-(-
)n]
tn=
,
vn=
,求解即可.
| a1 |
|
| ||
|
|
| ||
| 2 |
| π |
| 4n(n-1)θn |
| 1 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
1-(-
| ||
1-(-
|
| 4 |
| 5 |
| 1 |
| 4 |
1-(-
| ||
1-(-
|
| 8 |
| 5 |
| 1 |
| 4 |
| lim |
| n→∞ |
| 4 |
| 5 |
| lim |
| n→∞ |
| 8 |
| 5 |
解答:
解:(1)|
|=
=
=
|
|,
∵|
|≠0,
=
∴数列{|
|}是等比数列
(2)∵cosθn=
=
=
=
,
∴θn=
,n≥2,
∴bn=
=
=
-
,
∴Sn=b1+b2+b3+…+bn=1-
,n≥2,
(3)
=(1,2),
=(-
,
),
=(-1,
),
=(-
,
),
=(-
,-
)=-
(1,2)
∴
∥
∥
∥…
即
=
,
=(-
)n-1(1,2)
∴tn=
=
[1-(-
)n],vn=2×
=
[1-(-
)n]
∴
tn=
,
vn=
∴极限点D的坐标(
,
)
| an |
| 1 |
| 2 |
| (xn-1-yn-1)2+(xn-1+yn-1)2 |
| ||
| 2 |
|
| ||
| 2 |
| an-1 |
∵|
| a1 |
|
| ||
|
|
| ||
| 2 |
∴数列{|
| an |
(2)∵cosθn=
| ||||
|
|
(xn-1,yn-1)•
| ||||||
|
=
| ||||||||
|
| ||
| 2 |
∴θn=
| π |
| 4 |
∴bn=
| π |
| 4n(n-1)θn |
| 1 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
∴Sn=b1+b2+b3+…+bn=1-
| 1 |
| n |
(3)
| a1 |
| a2 |
| 1 |
| 2 |
| 3 |
| 2 |
| a3 |
| 1 |
| 2 |
| a4 |
| 1 |
| 2 |
| 3 |
| 2 |
| a5 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴
| a1 |
| a5 |
| a9 |
即
| dn |
| a4n-3 |
| dn |
| 1 |
| 4 |
∴tn=
1-(-
| ||
1-(-
|
| 4 |
| 5 |
| 1 |
| 4 |
1-(-
| ||
1-(-
|
| 8 |
| 5 |
| 1 |
| 4 |
∴
| lim |
| n→∞ |
| 4 |
| 5 |
| lim |
| n→∞ |
| 8 |
| 5 |
∴极限点D的坐标(
| 4 |
| 5 |
| 8 |
| 5 |
点评:本题综合考查了数列的性质,求和公式,裂项的思想,属于综合题.

练习册系列答案
相关题目
函数f(x)=lgx-
的零点个数为( )
| 1 |
| x |
| A、0 | B、1 | C、2 | D、3 |
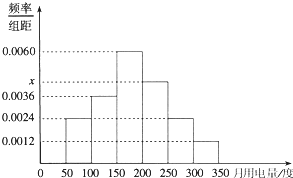 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.求
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.求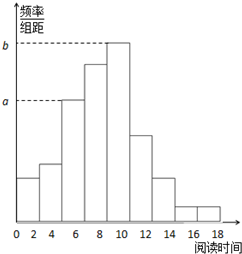 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图: