题目内容
依次计算a1=2×(1-
),a2=2×(1-
)(1-
),a3=2×(1-
)(1-
)(1-
),a4=2×(1-
)(1-
)(1-
)(1-
),猜想an=2×(1-
)(1-
)(1-
)…(1-
)结果并用数学归纳法证明你的结论.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 16 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 16 |
| 1 |
| 25 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 16 |
| 1 |
| (n+1)2 |
考点:数学归纳法
专题:证明题,点列、递归数列与数学归纳法
分析:先计算、猜想,再利用数学归纳法进行证明.
解答:
解:a1=2×(1-
)=
,a2=2×(1-
)(1-
)=
,a3=2×(1-
)(1-
)(1-
)=
,a4=2×(1-
)(1-
)(1-
)(1-
)=
,
猜想:an=
证明:(1)当n=1时,显然成立;
(2)假设当n=k(k∈N+)命题成立,即ak=
则当n=k+1时,ak+1=ak•[1-
]=
∴命题成立
由(1)(2)可知,an=
对n∈N+成立.
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 1 |
| 9 |
| 4 |
| 3 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 16 |
| 5 |
| 4 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 16 |
| 1 |
| 25 |
| 6 |
| 5 |
猜想:an=
| n+2 |
| n+1 |
证明:(1)当n=1时,显然成立;
(2)假设当n=k(k∈N+)命题成立,即ak=
| k+2 |
| k+1 |
则当n=k+1时,ak+1=ak•[1-
| 1 |
| (k+2)2 |
| k+3 |
| k+2 |
∴命题成立
由(1)(2)可知,an=
| n+2 |
| n+1 |
点评:本题考查归纳猜想,考查数学归纳法证明等式,解题的关键是先猜后证.

练习册系列答案
相关题目
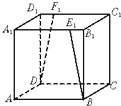 如图,正方体ABCD-A1B1C1D1中,E1、F1分别是A1B1、C1D1上的点,并且4B1E1=4D1F1=A1B1,则BE1与DF1所成角的余弦值是( )
如图,正方体ABCD-A1B1C1D1中,E1、F1分别是A1B1、C1D1上的点,并且4B1E1=4D1F1=A1B1,则BE1与DF1所成角的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
