题目内容
若对于任意实数x不等式x+|x-2m|＞4恒成立，则实数m的取值范围是： ．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：由题意可得|x-2m|＞4-x恒成立，函数y=|x-2m|的图象横在直线y=4-x的上方，数形结合求得实数m的取值范围．
解答：
解：由题意可得|x-2m|＞4-x恒成立，
故函数y=|x-2m|的图象横在直线y=4-x的上方，
如图所示：故有2m＞4，解得m＞2，
故答案为：（2，+∞）．
解：由题意可得|x-2m|＞4-x恒成立，故函数y=|x-2m|的图象横在直线y=4-x的上方，
如图所示：故有2m＞4，解得m＞2，
故答案为：（2，+∞）．
点评：本题主要考查带由绝对值的函数，体现了转化、数形结合的数学思想，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
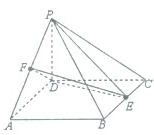如图，四棱锥P-ABCD的底面ABCD为菱形，PD⊥平面ABCD，PD=AB=2，∠BAD=60°，E、F分别为BC、PA的中点．
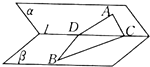已知二面角α-l-β的大小为60°，A∈α，B∈β，AC⊥l于C，BD⊥l于D，AC=BD=4，CD=3，则AD与BC所成角的余弦值为