题目内容
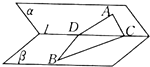 已知二面角α-l-β的大小为60°,A∈α,B∈β,AC⊥l于C,BD⊥l于D,AC=BD=4,CD=3,则AD与BC所成角的余弦值为
已知二面角α-l-β的大小为60°,A∈α,B∈β,AC⊥l于C,BD⊥l于D,AC=BD=4,CD=3,则AD与BC所成角的余弦值为考点:异面直线及其所成的角
专题:空间角
分析:由于
=
+
+
,利用数量积的性质可得:
2=
2+
2+
2+2
•
+2
•
+2
•
,把已知代入即可得出.
| AC |
| AD |
| DB |
| BC |
| AC |
| AD |
| DB |
| BC |
| AD |
| DB |
| AD |
| BC |
| DB |
| BC |
解答:
解:如图所示,过D在平面α内作DE⊥l,过A作AE∥l,DE∩AE=E,BE,AB.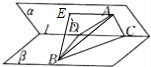
则∠BDE是二面角α-l-β,其大小为60°,DE=AC=4,AE=CD=3.
∴△BDE是等边三角形.
由上面可知:l⊥平面BDE,AE∥l.
∴AE⊥平面BDE.
∴AE⊥BE.
∴AB=
=5.
∵
=
+
+
,
∴
2=
2+
2+
2+2
•
+2
•
+2
•
.
∵AD=
=5,同理可得BC=5.
•
=-
•
=-9,
•
=-
•
=-9.
∴52=52+32+52-2×9+2
•
-2×9,
∴
•
=1,
∴5×5cos<
,
>=
∴异面直线AD与BC所成角的余弦值为
.
故答案为:
.

则∠BDE是二面角α-l-β,其大小为60°,DE=AC=4,AE=CD=3.
∴△BDE是等边三角形.
由上面可知:l⊥平面BDE,AE∥l.
∴AE⊥平面BDE.
∴AE⊥BE.
∴AB=
| BE2+AE2 |
∵
| AB |
| AD |
| DC |
| CB |
∴
| AB |
| AD |
| DC |
| CB |
| AD |
| DC |
| AD |
| CB |
| DC |
| CB |
∵AD=
| CD2+AC2 |
| AD |
| DC |
| DA |
| DC |
| DC |
| CB |
| CD |
| CB |
∴52=52+32+52-2×9+2
| AD |
| CB |
∴
| AD |
| CB |
∴5×5cos<
| AD |
| CB |
| 1 |
| 25 |
∴异面直线AD与BC所成角的余弦值为
| 1 |
| 25 |
故答案为:
| 1 |
| 25 |
点评:本题考查了向量的多边形法则、数量积的性质、异面直线所成的角等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
已知
,
为单位向量,且满足(2
+
)•
=0,则<
,
>=( )
| e1 |
| e2 |
| e1 |
| e2 |
| e2 |
| e1 |
| e2 |
| A、30° | B、60° |
| C、120° | D、150° |
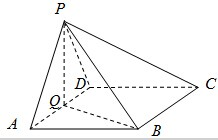 如图四棱锥P-ABCD的底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图四棱锥P-ABCD的底面ABCD为菱形,∠BAD=60°,Q为AD的中点.