题目内容

设f（x）=ax2+bx+c，?x，有：①f（x）≥0，②f′（0）＞0，则
f(2)
f′(0)
的最小值为
 
．
考点：导数的运算,二次函数的性质
专题：函数的性质及应用
分析：由题意，求出a、b、c满足的条件是什么，化简
f(2)
f′(0)
，求出它的最小值是什么．
解答： 解：根据题意，得；
∵①f（x）≥0，
∴
a＞0
b2-4ac≤0
；
∵②f′（0）＞0，
∴f′（x）=2ax+b，
∴f′（0）=b＞0；
∴
a＞0
b＞0
c≥
b2
4a
；
∴
f(2)
f′(0)
=
4a+2b+c
b
≥
4a
b
+2+
b2
4ab

=
4a
b
+
b
4a
+2≥2
4a
b
•
b
4a
+2=4，
当且仅当b=4a时，“=”成立；
∴
f(2)
f′(0)
的最小值为4．
故答案为：4．
点评：本题考查了二次函数的图象与性质的应用问题，解题时应根据题意，得出系数a、b、c满足的条件是什么，从而建立目标式，利用基本不等式，求出最值，是中档题．
练习册系列答案
相关题目
△ABC中，
5
sin2A-（2
5
+1）sinA+2=0，A是锐角，求cot2A的值．
有下列命题：
①在函数y=cos（x-
π
4
）cos（x+
π
4
）的图象中，相邻两个对称中心的距离为
π
2
；
②若锐角α，β满足cosα＞sinβ，则α+β＜
π
2
；
③若α，β均为第一象限角，且α＞β，则sinα＞sinβ；
④要得到函数y=sin（
x
2
-
π
4
）的图象，只需将y=sin
x
2
的图象向右平移
π
4
个单位；
则以上所有真命题的序号是
 
．
焦点在x轴的椭圆
x2
4a
+
y2
a2+1
=1（a＞0），则它的离心率的取值范围为
 
．
若对于任意实数x不等式x+|x-2m|＞4恒成立，则实数m的取值范围是：
 
．
函数f（x）=x2+x+1（x∈[1，4]）的值域为
 
．
函数f（x）=-x2+3x-2的两个零点是
 
．
表面积为324π的球，其内接长方体的高是14，且底面是正方形，则这个长方体的表面积为
 
．
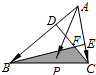如图，D、E是△ABC边AB、AC上的点，已知AB=3AD，AE=2EC，BE交CD于点F，点P是△FBC内（含边界）一点，若
AP
=λ
AB
+μ
AE
，则λ+μ的取值范围是（　　）
A、[
3
4
，1]
B、[
2
3
，1]
C、[1，
3
2
]
D、[1，2]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网