题目内容
已知双曲线C:
-
=1(b>0)的一条渐进线方程为y=
x,F1,F2分别为双曲线C的左右焦点,P为双曲线C上的一点,满足|PF1|:|PF2|=3:1,则|
+
|的值是( )
| x2 |
| 4 |
| y2 |
| b2 |
| ||
| 2 |
| PF1 |
| PF2 |
| A、4 | ||||
B、2
| ||||
C、2
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用双曲线C:
-
=1(b>0)的一条渐近线方程为y=
x,求出b,c,利用|PF1|:|PF2|=3:1,可得|PF1|=6,|PF2|=2,再求|
+
|即可.
| x2 |
| 4 |
| y2 |
| b2 |
| ||
| 2 |
| PF1 |
| PF2 |
解答:
解:∵双曲线C:
-
=1(b>0)的一条渐近线方程为y=
x,
∴b=
,
∴c=
,
∵|PF1|:|PF2|=3:1,
∴|PF1|=6,|PF2|=2,
∴cos∠F1PF2=
=0,
∴|
+
|2=36+4=40,
∴|
+
|=2
.
故选:C.
| x2 |
| 4 |
| y2 |
| b2 |
| ||
| 2 |
∴b=
| 6 |
∴c=
| 10 |
∵|PF1|:|PF2|=3:1,
∴|PF1|=6,|PF2|=2,
∴cos∠F1PF2=
| 36+4-40 |
| 2×6×2 |
∴|
| PF1 |
| PF2 |
∴|
| PF1 |
| PF2 |
| 10 |
故选:C.
点评:本题考查双曲线的性质,考查向量知识的运用,确定双曲线方程是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设m、n是两条不同的直线,α、β是两个不平的平面,下列命题中正确的是( )
| A、若α⊥β,α∩β=n,m⊥n,则m⊥α |
| B、若α∥β,m∥α,n∥β,则m∥n |
| C、若α⊥β,m?α,n?β,m⊥n,则m⊥β |
| D、若α⊥β,m⊥α,m∥n,n?β,则n∥β |
函数f(x)=
的最大值为M,最小值为N,则( )
| ||||
| 2x2+cosx |
| A、M-N=4 |
| B、M+N=4 |
| C、M-N=2 |
| D、M+N=2 |
已知
,
为单位向量,且满足(2
+
)•
=0,则<
,
>=( )
| e1 |
| e2 |
| e1 |
| e2 |
| e2 |
| e1 |
| e2 |
| A、30° | B、60° |
| C、120° | D、150° |
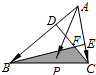 如图,D、E是△ABC边AB、AC上的点,已知AB=3AD,AE=2EC,BE交CD于点F,点P是△FBC内(含边界)一点,若
如图,D、E是△ABC边AB、AC上的点,已知AB=3AD,AE=2EC,BE交CD于点F,点P是△FBC内(含边界)一点,若| AP |
| AB |
| AE |
A、[
| ||
B、[
| ||
C、[1,
| ||
| D、[1,2] |
若实数a,b,c成等比数列,非零实数x,y分别为a与b,b与c的等差中项,则下列结论正确的是( )
A、
| ||||
B、
| ||||
| C、ax+cy=1 | ||||
| D、ax+cy=2 |
已知数列{an}中,a1=2,nan+1=(n+1)an+2,n∈N+,则a11=( )
| A、36 | B、38 | C、40 | D、42 |