题目内容
已知f(x)=log2x+2,x∈[1,4],则函数F(x)=[f(x)]2+f(x2)+3的最大值为( )
| A、13 | B、16 | C、25 | D、22 |
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:求解出定义域:[1,2],换元转化g(t)=t2+6t+9,t∈[0,1],根据二次函数性质求解.
解答:
解:∵f(x)=log2x+2,x∈[1,4],
∴F(x)=[f(x)]2+f(x2)+3的定义域:[1,2]
设t=log2x则t∈[0,1]
∴函数F(x)=[f(x)]2+f(x2)+3=(log2x)2+6log2x+9
即根据二次函数性质得出最大值为g(1)=16,
故选:B
∴F(x)=[f(x)]2+f(x2)+3的定义域:[1,2]
设t=log2x则t∈[0,1]
∴函数F(x)=[f(x)]2+f(x2)+3=(log2x)2+6log2x+9
即根据二次函数性质得出最大值为g(1)=16,
故选:B
点评:本题考察了对数函数的性质,二次函数的性质,换元法求解最大值问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=lnx+
-1的零点个数为( )
| 1 |
| x |
| A、0 | B、1 | C、2 | D、3 |
已知函数f(x)=ax5-bx3+cx-3,f(-3)=7,则f(3)的值为( )
| A、13 | B、7 | C、-13 | D、-7 |
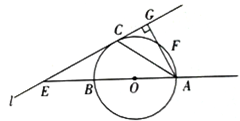 已知:直线AB过圆心O,交⊙O于A、B,直线AF交⊙O于A、F(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
已知:直线AB过圆心O,交⊙O于A、B,直线AF交⊙O于A、F(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.