Question

已知三棱锥S-ABC的各顶点都在一个半径为1的球面上，球心O在AB上，SO⊥面ABC，AC=

2

，则该三棱锥的表面积为

 

．

Answer 1

考点：棱柱、棱锥、棱台的侧面积和表面积

专题：计算题,空间位置关系与距离

分析：根据题意得出棱锥的棱长，判断三角形的形状，运用面积公式求解即可．

解答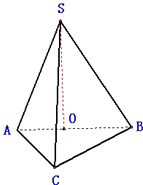： 解：如图，已知三棱锥S-ABC的各顶点都在一个半径为1的球面上，球心O在AB上，
SO⊥底面ABC，AC=

2

，AB=2，∠ACB=90°，BC=

2

，
∵SO⊥面ABC，
∴SO⊥AB，
∵OC=OS=OA=OB=1，
∴SA=SB=SC=

2

，
∴△SAC，△SBC为正三角形，
∴S_△ABC=

1

2

×

2

×

2

=1，S_△SAB=S_△SBC=

3

4

×（

2

）²=

3

2

，
∴该三棱锥的表面积为1+

3

2

+

3

2

=1+

3

，
故答案为：1+

3

点评：本题考查球的内接体和球的有关的计算问题，注意转化思想的应用，是基础题．