题目内容
经过点M(2,1)作直线l,交椭圆
+
=1于A,B两点,如果点M恰好为线段AB的中点,求直线l的方程.
| x2 |
| 16 |
| y2 |
| 4 |
考点:椭圆的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:设A(x1,y1),B(x2,y2),代入椭圆方程,作差运用平方差公式,结合中点坐标公式和直线的斜率公式,求出斜率,运用点斜式方程,求出直线方程,再检验与椭圆方程,消去x,得到y的方程,即可判断.
解答:
解:设A(x1,y1),B(x2,y2),
则
+
=1,
+
=1,
两式相减,可得,
+
=0,
又点M恰好为线段AB的中点,则x1+x2=4,y1+y2=2,
则直线l的斜率k=
=-
=-
,
则有直线l:y-1=-
(x-2).即为x+2y-4=0.
联立椭圆方程x2+4y2=16,消去x,得到8y2-16y=0,方程有两解,
则所求直线为x+2y-4=0.
则
| x12 |
| 16 |
| y12 |
| 4 |
| x22 |
| 16 |
| y22 |
| 4 |
两式相减,可得,
| (x1-x2)(x1+x2) |
| 16 |
| (y1-y2)(y1+y2) |
| 4 |
又点M恰好为线段AB的中点,则x1+x2=4,y1+y2=2,
则直线l的斜率k=
| y1-y2 |
| x1-x2 |
| x1+x2 |
| 4(y1+y2) |
| 1 |
| 2 |
则有直线l:y-1=-
| 1 |
| 2 |
联立椭圆方程x2+4y2=16,消去x,得到8y2-16y=0,方程有两解,
则所求直线为x+2y-4=0.
点评:本题考查点差法求中点弦所在直线方程,考查直线的斜率公式,及中点坐标公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
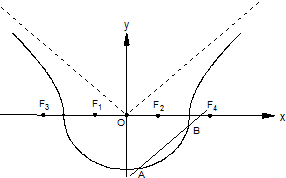 如图,曲线Γ由曲线C1:
如图,曲线Γ由曲线C1: