Question

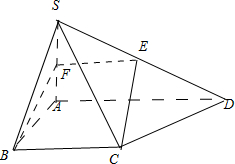在四棱锥S-ABCD中，底面ABCD为直角梯形，其中AD∥BC，∠BAD=90°，SA⊥底面ABCD，SA=AB=BC=2，tan∠SDA=

1

2

，E为SD的中点．
（Ⅰ）求证：CE∥平面SAB；
（Ⅱ）求三棱锥D-AEC的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定

专题：空间位置关系与距离

分析：（Ⅰ）取SA中点F，连接EF，BF，CE，得出EF=

1

3

AD=2，EF∥AD，AD∥BC，判断四边形EFBC为平行四边形，即可得出BF∥CE，
运用直线平面的平行的平判定定理BF∥CE，BF?平面SAB；CE?平面SAB可证明．
（Ⅱ）V_D-AEC=V_E-ACD，很容易求解：E到面ACD的距离为

1

2

×2=1，S_△ACD=

1

2

×4×2，运用体积公式求解即可．

解答： （Ⅰ）证明：∵SA⊥底面ABCD，
∴Rt△SDC中，tan∠SAD，tan∠SDA=

SA

AD

=

1

2

，
取SA中点F，连接EF，BF，CE，
∵SA=AB=BC=2，
∴AD=4，
EF=

1

3

AD=2，EF∥AD，
∵AD∥BC，
∴EF=BC，EF∥CB，
∴四边形EFBC为平行四边形，
∴BF∥CE，
∵BF?平面SAB；CE?平面SAB；
∴CE∥平面SAB；

（Ⅱ）∵SA⊥底面ABCD，E为SD的中点．
∴E到面ACD的距离为

1

2

×2=1，
S_△ACD=

1

2

×4×2
V_D-AEC=V_E-ACD=

1

3

×

1

2

×4×2×1=

4

3

，

点评：本题考查直线与平面平行的证明，考查了直线平面的夹角，解题时要认真审题，仔细解答，注意合理地化空间问题为平面问题．