题目内容
在△ABC中，角A、B、C的对边分别是a、b、c且满足（2a-c）cosB=bcosC．
（1）求B；
（2）若b=
，△ABC的周长为l，求l的最大值并判断此时△ABC的形状．
（1）求B；
（2）若b=
| 3 |
考点：正弦定理,余弦定理
专题：解三角形
分析：（1）由正弦定理、两角和的正弦公式化简（2a-c）cosB=bcosC，求出cosB的值，结合内角的范围求出B；
（2）由（1）和内角和定理可得A、C的关系及A的范围，由正弦定理求出
的值，代入三角形的周长l利用两角差与和的正弦公式化简，由A的范围和正弦函数的性质，求出l的最大值并判断此时△ABC的形状．
（2）由（1）和内角和定理可得A、C的关系及A的范围，由正弦定理求出
| b |
| sinB |
解答：
解：（1）由题意得，（2a-c）cosB=bcosC，
由正弦定理得（2sinA-sinC）cosB=sinBsinC，
2sinAcosB=sinBsinC+cosBsinC=sin（B+C）
因为A+B+C=π，所以2sinAcosB=sinA，
因为0＜A＜π，所以sinA≠0，则cosB=
，
由0＜B＜π得，B=
；
（2）由（1）得，A+C=π-B=
，则C=
-A，
设△ABC的外接圆的半径为R，
又b=
，由正弦定理得2R=
=
=2，
则△ABC的周长为l=a+b+c=2（sinA+sinB+sinC）
=2（sinA+sinC+
）=2[sinA+sin（
-A）]+
=2[sinA+sin
cosA-cos
sinA）]+
=2（
sinA+
cosA）+
=2
sin(A+
)+
，
因为C=
-A＞0，所以0＜A＜
，则
＜A+
＜
，
则当A+
=
时，l取到最大值3
，
此时A=
，△ABC是等边三角形．
由正弦定理得（2sinA-sinC）cosB=sinBsinC，
2sinAcosB=sinBsinC+cosBsinC=sin（B+C）
因为A+B+C=π，所以2sinAcosB=sinA，
因为0＜A＜π，所以sinA≠0，则cosB=
| 1 |
| 2 |
由0＜B＜π得，B=
| π |
| 3 |
（2）由（1）得，A+C=π-B=
| 2π |
| 3 |
| 2π |
| 3 |
设△ABC的外接圆的半径为R，
又b=
| 3 |
| b |
| sinB |
| ||
sin
|
则△ABC的周长为l=a+b+c=2（sinA+sinB+sinC）
=2（sinA+sinC+
| ||
| 2 |
| 2π |
| 3 |
| 3 |
=2[sinA+sin
| 2π |
| 3 |
| 2π |
| 3 |
| 3 |
=2（
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| π |
| 6 |
| 3 |
因为C=
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
则当A+
| π |
| 6 |
| π |
| 2 |
| 3 |
此时A=
| π |
| 3 |
点评：本题考查正弦定理，两角差与和的正弦公式，以及正弦函数的性质，属于中档题．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
已知角α的终边经过点P（-4，-3），则sinα的值为（ ）
A、-
| ||
B、-
| ||
C、
| ||
D、
|
若全集U={1，2，3，4，5，6}，M={1，4}，N={2，3}，则集合（∁UM）∩N等于（ ）
| A、{2，3} |
| B、{2，3，5，6} |
| C、{1，4} |
| D、{1，4，5，6} |
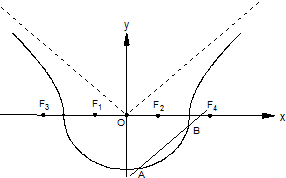如图，曲线Γ由曲线C1：