题目内容
已知函数f(x)=
的定义域为A,
(1)求A;
(2)若B={x|x2-2x+1-k2≥0},且A∩B≠∅,求实数k的取值范围.
| lg(x2-2x) | ||
|
(1)求A;
(2)若B={x|x2-2x+1-k2≥0},且A∩B≠∅,求实数k的取值范围.
考点:一元二次不等式的解法,交集及其运算,函数的定义域及其求法
专题:函数的性质及应用,不等式的解法及应用,集合
分析:(1)由题意,函数的定义域满足真数大于0,且分母不为0,二次根式的被开方数大于或等于0,由此列出不等式组,解即可;
(2)对集合B,解不等式x2-2x+1-k2≥0,并对k进行分类讨论,由A∩B≠∅求出k的取值范围.
(2)对集合B,解不等式x2-2x+1-k2≥0,并对k进行分类讨论,由A∩B≠∅求出k的取值范围.
解答:
解:(1)由题意,得
;
解得-3<x<0,或2<x<3,
∴函数的定义域为
A=(-3,0)∪(2,3);
(2)∵x2-2x+1-k2≥0,
∴当k≥0时,x≤1-k或x≥1+k,
当k<0时,x≤1+k或x≥1-k;
又∵A∩B≠∅,
∴
,或
,
或
,或
;
解得k∈[-4,4].
|
解得-3<x<0,或2<x<3,
∴函数的定义域为
A=(-3,0)∪(2,3);
(2)∵x2-2x+1-k2≥0,
∴当k≥0时,x≤1-k或x≥1+k,
当k<0时,x≤1+k或x≥1-k;
又∵A∩B≠∅,
∴
|
|
或
|
|
解得k∈[-4,4].
点评:本题考查了求函数的定义域以及一元二次不等式的解法问题,也考查了集合的简单运算与分类讨论思想,是综合性题目.

练习册系列答案
相关题目
在平面直角坐标系中,x轴的正半轴上有4个点,y轴的正半轴上有5个点,这9个点任意两点连线,则所有连线段的交点落入第一象限的个数最多是( )
| A、30 | B、60 |
| C、120 | D、240 |

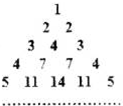 用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aij=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行中的各数之和为bn.
用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aij=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行中的各数之和为bn. 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,