题目内容
已知函数f(x)=sin2ωx+
sinωxsin(ωx+
)+2cos2ωx,x∈R(ω>0),在y轴右侧的第一个最高点的横坐标为
.若将函数f(x)的图象向右平移
个单位后,再将得到的图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)的图象.
(1)求函数g(x)的最大值及单调递减区间.
(2)(文)在△ABC中,a,b,c分别是角A,B,C的对边,a=
,b+c=3且f(A)=2,求角A的值.
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
(1)求函数g(x)的最大值及单调递减区间.
(2)(文)在△ABC中,a,b,c分别是角A,B,C的对边,a=
| 3 |
考点:正弦定理,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的求值
分析:(1)f(x)解析式利用诱导公式及二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据在y轴右侧的第一个最高点的横坐标为
,求出ω的值,确定出f(x)解析式,再利用平移规律确定出g(x)解析式,根据正弦函数的值域及单调性即可确定出函数g(x)的最大值及单调递减区间;
(2)由f(A)=2及(1)得出的f(x)解析式,求出A的度数即可.
| π |
| 6 |
(2)由f(A)=2及(1)得出的f(x)解析式,求出A的度数即可.
解答:
解:(1)f(x)=
sin2ωx+
cos2ωx+
=sin(2ωx+
)+
,
令2ωx+
=
,将x=
代入可得:ω=1,
∴f(x)=sin(2x+
)+
,函数g(x)=sin(x-
)+
,
当x=2kπ+
π,k∈Z时,函数取得最大值
,
令2kπ+
≤x-
≤2kπ+
π,即x∈[2kπ+
π,2kπ+
π],k∈Z为函数的单调递减区间;
(2)f(x)=sin(2x+
)+
,
∵f(A)=2,
∴sin(2A+
)=
,
∵0<A<π,即
<2A+
<
π,
∴2A+
=
π,
∴A=
.
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| π |
| 6 |
| 3 |
| 2 |
令2ωx+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
∴f(x)=sin(2x+
| π |
| 6 |
| 3 |
| 2 |
| π |
| 6 |
| 3 |
| 2 |
当x=2kπ+
| 2 |
| 3 |
| 5 |
| 2 |
令2kπ+
| π |
| 2 |
| π |
| 6 |
| 3 |
| 2 |
| 2 |
| 3 |
| 5 |
| 3 |
(2)f(x)=sin(2x+
| π |
| 6 |
| 3 |
| 2 |
∵f(A)=2,
∴sin(2A+
| π |
| 6 |
| 1 |
| 2 |
∵0<A<π,即
| π |
| 6 |
| π |
| 6 |
| 13 |
| 6 |
∴2A+
| π |
| 6 |
| 5 |
| 6 |
∴A=
| π |
| 3 |
点评:此题考查了正弦定理,诱导公式,二倍角的正弦、余弦函数公式,正弦函数的单调性及值域,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
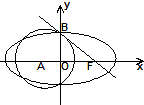 如图,已知点F为椭圆C:
如图,已知点F为椭圆C: 已知四棱锥P-ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.