题目内容
圆心角为60°的扇形面积为6π，求它围成的圆锥的表面积．
考点：扇形面积公式
专题：计算题,空间位置关系与距离
分析：设扇形的半径和圆锥的母线都为l，圆锥的半径为r，利用扇形的面积公式与弧长公式求得l，r；再利用勾股定理求圆锥的高，代入面积公式和体积公式计算可得答案．
解答：
解：设扇形的半径和圆锥的母线都为l，圆锥的半径为r，
则
πl2=6π，解得l=6；
∵
×6=2πr，
∴r=1；
∴S表面积=S侧面+S底面=πrl+πr2=7π．
则
| 60 |
| 360 |
∵
| π |
| 3 |
∴r=1；
∴S表面积=S侧面+S底面=πrl+πr2=7π．
点评：本题考查了圆锥的侧面展开图及侧面积公式，考查了扇形的弧长公式及圆的周长公式，关键是结合图形求底面圆的半径，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
下列函数中，最小正周期为π的偶函数是（ ）
| A、y=sin2x | ||
B、y=cos
| ||
C、y=
| ||
| D、y=sin2x+cos2x |
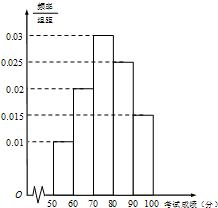某市为了了解本市高中学生的汉字书写水平，在全市范围内随机抽取了近千名学生参加汉字听写考试，将所得数据整理后，绘制出频率分布直方图如图所示，其中样本数据分组区间为[50，60），[60，70），[70，80），[80，90），[90，100]．