题目内容
已知α,β是两个不同平面,m,n是两条不同直线,则以下命题正确的是( )
| A、若m∥n,n?α,则m∥α |
| B、若m∥α,m∥β,则α∥β |
| C、若m∥α,n∥α,则m∥n |
| D、若m∥α,m?β,α∩β=n,则m∥n |
考点:空间中直线与平面之间的位置关系,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用线面平行的性质定理和判定定理对四个选项分别分析解答.
解答:
解:对于A,若m∥n,n?α,则m可能在α内;故A错误;
对于B,若m∥α,m∥β,则α与β可能相交;故B错误;
对于C,若m∥α,n∥α,则m与n的位置关系可能为相交、平行或者异面;故C错误;
对于D,若m∥α,m?β,α∩β=n,根据线面平行的性质定理可以得到m∥n;故D正确;
故选D.
对于B,若m∥α,m∥β,则α与β可能相交;故B错误;
对于C,若m∥α,n∥α,则m与n的位置关系可能为相交、平行或者异面;故C错误;
对于D,若m∥α,m?β,α∩β=n,根据线面平行的性质定理可以得到m∥n;故D正确;
故选D.
点评:本题考查了线面平行的性质定理和判定定理;熟练的掌握定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知l,m,n是三条不同的直线,α,β,γ是三个不同的平面,下面命题正确的是( )
| A、若m⊥l,n⊥l,则m∥n |
| B、若α⊥γ,β⊥γ,则α∥β |
| C、若m∥l,n∥l,则m∥n |
| D、若m∥α,n∥α,则m∥n |
如果二次函数f(x)=3x2+bx+1的图象关于直线x=
对称,则b的值为( )
| 1 |
| 2 |
| A、-1 | B、1 | C、-3 | D、3 |
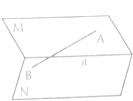 二面角M-a-N中,点A∈M,点B∈N,AB=4
二面角M-a-N中,点A∈M,点B∈N,AB=4