题目内容
函数f(x)=msinx+
cosx(m>0)的最大值为2,求在[0,π]的单调减区间.
| 2 |
考点:三角函数的最值
专题:计算题,三角函数的求值,三角函数的图像与性质
分析:将f(x)解析式利用两角和与差的正弦函数公式化为一个角的正弦函数,由正弦函数的值域表示出f(x)的最大值,由已知最大值为2列出关于m的方程,求出方程的解得到m的值,进而确定出f(x)的解析式,由正弦函数的递减区间为[2kπ+
,2kπ+
](k∈Z),列出关于x的不等式,求出不等式的解集即可得到f(x)在[0,π]上的单调递减区间.
| π |
| 2 |
| 3π |
| 2 |
解答:
解:f(x)=msinx+
cosx=
sin(x+θ)(其中sinθ=
,cosθ=
),
∴f(x)的最大值为
,
∴
=2,
又m>0,∴m=
,
∴f(x)=2sin(x+
),
令2kπ+
≤x+
≤2kπ+
(k∈Z),解得:2kπ+
≤x≤2kπ+
(k∈Z),
则f(x)在[0,π]上的单调递减区间为[
,π].
| 2 |
| m2+2 |
| ||
|
| m | ||
|
∴f(x)的最大值为
| m2+2 |
∴
| m2+2 |
又m>0,∴m=
| 2 |
∴f(x)=2sin(x+
| π |
| 4 |
令2kπ+
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 4 |
| 5π |
| 4 |
则f(x)在[0,π]上的单调递减区间为[
| π |
| 4 |
点评:本题考查两角和与差的正弦函数公式,以及正弦函数的单调性,熟练掌握公式是解本题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
若定义在R上的函数f(x)满足f(x1+x2)=f(x1)+f(x2),则函数f(x)一定是( )
| A、奇函数 | B、偶函数 |
| C、减函数 | D、增函数 |
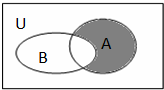
设全集U=R,A={x||x+1|<1},B={x|(
)x-2≥0},则图中阴影部分所表示的集合( )
| 1 |
| 2 |

| A、(-2,0) |
| B、(-2,-1] |
| C、(-1,0] |
| D、(-1,0) |
已知α,β是两个不同平面,m,n是两条不同直线,则以下命题正确的是( )
| A、若m∥n,n?α,则m∥α |
| B、若m∥α,m∥β,则α∥β |
| C、若m∥α,n∥α,则m∥n |
| D、若m∥α,m?β,α∩β=n,则m∥n |
某程序框图如图所示,若该程序运行后输出的值是
,则①处应填( )

| 3 |
| 4 |

| A、k<3 | B、k<4 |
| C、k>3 | D、k>4 |
