题目内容
实数R,集合A={x|-1≤x<3},B={x|2x-4≥0}.
(Ⅰ)求∁R(A∩B);
(Ⅱ)若集合C={x|y=log2(x-a)},且满足B∪C=C,求实数a的取值范围.
(Ⅰ)求∁R(A∩B);
(Ⅱ)若集合C={x|y=log2(x-a)},且满足B∪C=C,求实数a的取值范围.
考点:交、并、补集的混合运算
专题:集合
分析:(Ⅰ)先求出A∩B,再根据补集的运算法则计算即可
(Ⅱ)先根据对数函数的定义求出集合C,再根据B∪C=C,得到B⊆C,继而求出a的范围
(Ⅱ)先根据对数函数的定义求出集合C,再根据B∪C=C,得到B⊆C,继而求出a的范围
解答:
解:(Ⅰ)∵集合A={x|-1≤x<3},B={x|2x-4≥0}={x|x≥2}
∴A∩B={x|2≤x<3}
∴∁R(A∩B)={x|x<2,或x≥3}
(Ⅱ)∵集合C={x|y=log2(x-a)},
∴C={x|x>a}
∵B∪C=C,
∴B⊆C,
∴a<2
∴A∩B={x|2≤x<3}
∴∁R(A∩B)={x|x<2,或x≥3}
(Ⅱ)∵集合C={x|y=log2(x-a)},
∴C={x|x>a}
∵B∪C=C,
∴B⊆C,
∴a<2
点评:本题考查集合的交并补运算,属于基础题

练习册系列答案
相关题目
已知向量
=(2,1),
=(-1,k2-2),则k=2是
⊥
的( )
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知原命题:若a+b>2,则a,b至少有一个大于1,那么原命题与其逆命题的真假情况是( )
| A、原命题真,逆命题假 |
| B、原命题假,逆命题真 |
| C、原命题与逆命题均为真命题 |
| D、原命题与逆命题均为假命题 |
已知弧长28cm的弧所对圆心角为240°,则这条弧形所在扇形的面积为( )
| A、336π | ||
| B、294π | ||
C、
| ||
D、
|
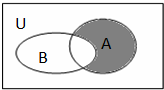
设全集U=R,A={x||x+1|<1},B={x|(
)x-2≥0},则图中阴影部分所表示的集合( )
| 1 |
| 2 |

| A、(-2,0) |
| B、(-2,-1] |
| C、(-1,0] |
| D、(-1,0) |
i为虚数单位,则
=( )
| i+1 |
| i-1 |
| A、1 | B、-i | C、i | D、-1 |
已知α,β是两个不同平面,m,n是两条不同直线,则以下命题正确的是( )
| A、若m∥n,n?α,则m∥α |
| B、若m∥α,m∥β,则α∥β |
| C、若m∥α,n∥α,则m∥n |
| D、若m∥α,m?β,α∩β=n,则m∥n |