题目内容
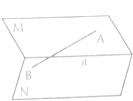二面角M-a-N中，点A∈M，点B∈N，AB=4| 2 |
| 2 |
考点：二面角的平面角及求法
专题：空间角
分析：过A作AC⊥a，交a于点C，过B作BD⊥a，交a于点C，连结AD，过B作BE∥DC，过C作CE∥BD，交BE于E，连结AE，则BECD是矩形，人而EC⊥a，进而得到∠ACE是二面角M-a-N的平面角，由此利用勾股定理和余弦定理能求出二面角M-a-N的平面角的大小．
解答：
解：过A作AC⊥a，交a于点C，过B作BD⊥a，交a于点C，
连结AD，
过B作BE∥DC，过C作CE∥BD，交BE于E，
连结AE，则AC=4，BD=2
，BECD是矩形，
∴EC⊥a，∴∠ACE是二面角M-a-N的平面角，
由已知得AD=
=
=2
，
BE=CD=
=
=2
，
∵AB与a所成的角是30°，∴∠ABE=30°，
∴AE=
=2
，
∴cos∠ACE=
=
．
∴∠ACE=arccos
．
∴二面角M-a-N的平面角为arccos
．
连结AD，过B作BE∥DC，过C作CE∥BD，交BE于E，
连结AE，则AC=4，BD=2
| 2 |
∴EC⊥a，∴∠ACE是二面角M-a-N的平面角，
由已知得AD=
| AB2-BD2 |
| 32-8 |
| 6 |
BE=CD=
| AD2-AC2 |
| 24-16 |
| 2 |
∵AB与a所成的角是30°，∴∠ABE=30°，
∴AE=
| AB2+BE2-2AB•BEcos30° |
=2
10-4
|
∴cos∠ACE=
| AC2+CE2-AE2 |
| 2AC•CE |
| ||||
| 2 |
∴∠ACE=arccos
| ||||
| 2 |
∴二面角M-a-N的平面角为arccos
| ||||
| 2 |
点评：本题考查二面角的平面角的大小的求法，涉及到线面平行、线面垂直的性质的应用，解题时要注意勾股定理、余弦定理的合理运用．
练习册系列答案
相关题目
某次考试结束后，从考号为1-1000号的1000份试卷中，采用系统抽样法抽取50份试卷进行试评，则在考号区间[850，949]之中被抽到的试卷份数为（ ）
| A、一定是5份 |
| B、可能是4份 |
| C、可能会有10份 |
| D、不能具体确定 |
已知弧长28cm的弧所对圆心角为240°，则这条弧形所在扇形的面积为（ ）
| A、336π | ||
| B、294π | ||
C、
| ||
D、
|
i为虚数单位，则
=（ ）
| i+1 |
| i-1 |
| A、1 | B、-i | C、i | D、-1 |
已知α，β是两个不同平面，m，n是两条不同直线，则以下命题正确的是（ ）
| A、若m∥n，n?α，则m∥α |
| B、若m∥α，m∥β，则α∥β |
| C、若m∥α，n∥α，则m∥n |
| D、若m∥α，m?β，α∩β=n，则m∥n |
设l，m是两条不同的直线，α，β是不同的平面，则下列命题正确的是（ ）
| A、若l⊥m，m?α，则l⊥α |
| B、若l∥α，m?α，则l∥m |
| C、若α∥β，l?α，则l∥β |
| D、若α⊥β，l?α，则l⊥β |