题目内容
若在△ABC中,AB=2,AC=
BC,求△ABC面积的最大值.
| 2 |
考点:余弦定理
专题:解三角形
分析:设BC=x则AC=
x,利用余弦定理求出cosB,求出cos2B和sin2B,再利用三角形的面积公式化简S△ABC2,利用配方法和二次函数的性质求出面积的最大值.
| 2 |
解答:
解:设BC=x,则AC=
x,
根据余弦定理得,cosB=
=
=
=
-
,
则cos2B=(
-
)2=
+
-
,sin2B=1-cos2B=
-
-
,
根据面积公式得,S△ABC=
AB•BCsinB=xsinB,
所以S△ABC2=x2sin2B=x2(
-
-
)=
x2-1-
=-
(x4-24x2)-1=-
(x2-12)2+8,
当x2=12,即x=2
时,此时2、2
、2
能组成三角形,
且S△ABC2取到最大值8,即△ABC面积的最大值是2
.
| 2 |
根据余弦定理得,cosB=
| AB2+BC2-AC2 |
| 2AB•BC |
| 4+x2-2x2 |
| 4x |
=
| 4-x2 |
| 4x |
| 1 |
| x |
| x |
| 4 |
则cos2B=(
| 1 |
| x |
| x |
| 4 |
| 1 |
| x2 |
| x2 |
| 16 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| x2 |
| x2 |
| 16 |
根据面积公式得,S△ABC=
| 1 |
| 2 |
所以S△ABC2=x2sin2B=x2(
| 3 |
| 2 |
| 1 |
| x2 |
| x2 |
| 16 |
| 3 |
| 2 |
| x4 |
| 16 |
=-
| 1 |
| 16 |
| 1 |
| 16 |
当x2=12,即x=2
| 3 |
| 3 |
| 6 |
且S△ABC2取到最大值8,即△ABC面积的最大值是2
| 2 |
点评:本题考查余弦定理,平方关系,三角形的而面积公式,以及转化思想与二次函数的性质,注意验证三角形存在的条件,属于中档题.

练习册系列答案
相关题目
“a>2”是“函数y=ax是增函数”的( )
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
设全集U=R,A={x||x+1|<1},B={x|(
)x-2≥0},则图中阴影部分所表示的集合( )
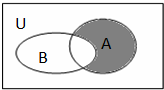
| 1 |
| 2 |

| A、(-2,0) |
| B、(-2,-1] |
| C、(-1,0] |
| D、(-1,0) |
i为虚数单位,则
=( )
| i+1 |
| i-1 |
| A、1 | B、-i | C、i | D、-1 |
已知α,β是两个不同平面,m,n是两条不同直线,则以下命题正确的是( )
| A、若m∥n,n?α,则m∥α |
| B、若m∥α,m∥β,则α∥β |
| C、若m∥α,n∥α,则m∥n |
| D、若m∥α,m?β,α∩β=n,则m∥n |