题目内容
已知函数y=
的值域为[0，+∞），则实数a的取值范围是 ．
| ax2+2ax+1 |
考点：函数的值域
专题：函数的性质及应用
分析：本题可以由函数的值域得到函数解析式满足条件，从而求出实数a的取值范围，得到本题结论．
解答：
解：记f（x）=ax2+2ax+1，
∵函数y=
的值域为[0，+∞），
∴f（x）=ax2+2ax+1的图象是抛物线，开口向上，与x轴公共点，
∴a＞0，且△=4a2-4a≥0，
∴a≥1．
∴实数a的取值范围是：[1，+∞）．
故答案为：[1，+∞）．
∵函数y=
| ax2+2ax+1 |
∴f（x）=ax2+2ax+1的图象是抛物线，开口向上，与x轴公共点，
∴a＞0，且△=4a2-4a≥0，
∴a≥1．
∴实数a的取值范围是：[1，+∞）．
故答案为：[1，+∞）．
点评：本题考查了函数的值域和内函数图象的关系，本题难度不大，属于基础题．
练习册系列答案
名校名卷单元同步训练测试题系列答案
相关题目
若l，m表示直线，α，β，γ表示平面，则下列命题不正确的是（ ）
| A、若l⊥m，l⊥α，m⊥β，则α⊥β |
| B、若l⊥m，l?α，m?β，则α⊥β |
| C、若α⊥γ，β∥γ，则α⊥β |
| D、若l∥m，l⊥α，m?β，则α⊥β |
双曲线y=
的焦距为（ ）
| 1 |
| x |
A、
| ||
B、2
| ||
| C、2 | ||
| D、4 |
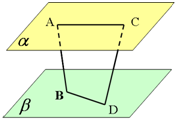已知AB、CD是夹在平行平面α、β间的异面线段，A，C∈α，B，D∈β，且AC=6，BD=8，AB=CD=10，AB和CD成60°角．求异面直线AC和BD所成的角．
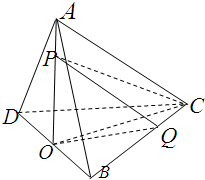如图，在三棱锥A-BCD中，BC=DC=AB=AD=2，BD=2，平面ABD⊥平面BCD，O为BD中点，点P，Q分别为线段AO，BC上的动点（不含端点），且AP=CQ，则三棱锥P-QCO体积的最大值为