题目内容
曲线y2-x-2y=0在二阶矩阵M=
的作用下变换为曲线y2=x;
(i)求实数a,b的值;
(ii)求M的逆矩阵M-1.
|
(i)求实数a,b的值;
(ii)求M的逆矩阵M-1.
考点:几种特殊的矩阵变换,逆矩阵与二元一次方程组
专题:矩阵和变换
分析:(1)利用矩阵变换可得
,代入新曲线y2=x,即可求得实数a,b的值;
(2)利用|M|=1及逆矩阵公式即可求得M的逆矩阵M-1.
|
(2)利用|M|=1及逆矩阵公式即可求得M的逆矩阵M-1.
解答:
(本小题满分7分)选修4-2:矩阵与变换
解:(1)由
=
得:
,
代入新曲线y2=x,得(bx+y)2=x+ay,即y2+2bxy+b2x2-x-ay=0
解得a=2,b=0,M=
…(4分)
(2)由(1)知M=
,|M|=1×1-0×2=1,其伴随矩阵M*=
(主对角线对换,副对角线符号相反),
由M-1=
得:M-1=
…(7分)
解:(1)由
|
|
|
|
代入新曲线y2=x,得(bx+y)2=x+ay,即y2+2bxy+b2x2-x-ay=0
解得a=2,b=0,M=
|
(2)由(1)知M=
|
|
由M-1=
| M* |
| |M| |
|
点评:本题考查矩阵变换及逆矩阵公式的应用,考查运算求解能力,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
已知集合A={1,3,5,7,9},B={0,3,6,9,12},则A∩(∁NB)=( )
| A、{1,2,3} |
| B、{1,3,9} |
| C、{1,5,7} |
| D、{3,5,7} |
已知点P是抛物线y2=4x上的动点,点P在y轴上的射影是M,点A 的坐标是(4,a),则当|a|>4时,|PA|+|PM|的最小值是( )
A、
| ||
B、
| ||
| C、a+3 | ||
D、
|
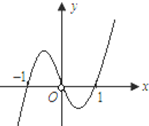 已知函数y=
已知函数y=| f′(x) |
| x |
| A、f′(1)=f′(-1)=0 |
| B、当x=-1时,函数f(x)取得极大值 |
| C、方程xf′(x)=0与f(x)=0均有三个实数根 |
| D、当x=1时,函数f(x)取得极小值 |