题目内容
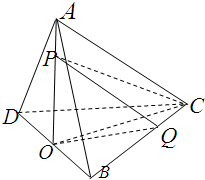 如图,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P-QCO体积的最大值为
如图,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P-QCO体积的最大值为考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:设出AP,表示出三棱锥P-QCO体积的表达式,然后求解最值即可.
解答:
解: 由题意,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,底面三角形BCD是正三角形,
由题意,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,底面三角形BCD是正三角形,
又∵平面ABD⊥平面BCD,O为BD中点,
可得AO⊥平面BCD,∴△AOC是直角三角形,
并且可得BD⊥平面AOC,
设AP=x,(x∈(0,1)),
三棱锥P-QCO体积为:V=
S△POC•h,
h为Q到平面AOC的距离,h=xsin30°=
x,
V=
S△POC•h=
×
×
(
-x)×
x=
(3x-
x2),
当x=
时,二次函数V=
(3x-
x2)取得最大值为:
故答案为:
.
 由题意,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,底面三角形BCD是正三角形,
由题意,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,底面三角形BCD是正三角形,又∵平面ABD⊥平面BCD,O为BD中点,
可得AO⊥平面BCD,∴△AOC是直角三角形,
并且可得BD⊥平面AOC,
设AP=x,(x∈(0,1)),
三棱锥P-QCO体积为:V=
| 1 |
| 3 |
h为Q到平面AOC的距离,h=xsin30°=
| 1 |
| 2 |
V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 12 |
| 3 |
当x=
| ||
| 2 |
| 1 |
| 12 |
| 3 |
| ||
| 16 |
故答案为:
| ||
| 16 |
点评:本题考查几何体的体积的最值的求法,正确路直线与平面垂直的判定定理以及平面余平米垂直的性质定理,表示出几何体的体积是解题的关键,考查转化思想以及计算能力.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
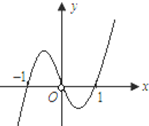 已知函数y=
已知函数y=| f′(x) |
| x |
| A、f′(1)=f′(-1)=0 |
| B、当x=-1时,函数f(x)取得极大值 |
| C、方程xf′(x)=0与f(x)=0均有三个实数根 |
| D、当x=1时,函数f(x)取得极小值 |
设函数f(x)的导函数为f′(x),对任意x∈R都有f(x)>f′(x)成立,则( )
| A、3f(ln2)>2f(ln3) |
| B、3f(ln2)=2f(ln3) |
| C、3f(ln2)<2f(ln3) |
| D、3f(ln2)与2f(ln3)的大小不确定 |
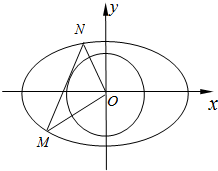 已知椭圆C:
已知椭圆C: