题目内容
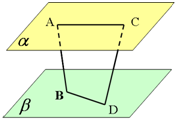已知AB、CD是夹在平行平面α、β间的异面线段，A，C∈α，B，D∈β，且AC=6，BD=8，AB=CD=10，AB和CD成60°角．求异面直线AC和BD所成的角．考点：异面直线及其所成的角
专题：计算题,作图题,空间位置关系与距离
分析：过C作CE∥AB交β于E，连接BE、DE，可知∠DBE（或其补角）即为AB和CD成的角，解三角形DBE．
解答：
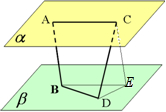解、过C作CE∥AB交β于E，连接BE、DE，
∵CE∥AB，
∴∠ECD即为AB和CD成的角，则∠ECD=60°，
又∵α∥β且CE∥AB，
∴CE=AB，则四边形ABEC为平行四边形，
∴AC∥BE，
∴∠DBE（或其补角）即为AB和CD成的角，
易知△CDE为正三角形，则DE=10，
∵AC=BE=6，BD=8，
∴∠DBE=90°．
即异面直线AC和BD所成的角为90°．
解、过C作CE∥AB交β于E，连接BE、DE，∵CE∥AB，
∴∠ECD即为AB和CD成的角，则∠ECD=60°，
又∵α∥β且CE∥AB，
∴CE=AB，则四边形ABEC为平行四边形，
∴AC∥BE，
∴∠DBE（或其补角）即为AB和CD成的角，
易知△CDE为正三角形，则DE=10，
∵AC=BE=6，BD=8，
∴∠DBE=90°．
即异面直线AC和BD所成的角为90°．
点评：本题考查了空间中角的求法，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知a，b，c分别是△ABC中∠A，∠B，∠C的对边，且（sinB+sinC+sinA）（sinB+sinC-sinA）=
sinBsinC，则以下结论中正确的是（ ）
| 18 |
| 5 |
A、cosA=
| ||
B、cosA=-
| ||
C、cosB=
| ||
D、cosB=-
|
已知集合A={1，3，5，7，9}，B={0，3，6，9，12}，则A∩（∁NB）=（ ）
| A、{1，2，3} |
| B、{1，3，9} |
| C、{1，5，7} |
| D、{3，5，7} |
已知点P是抛物线y2=4x上的动点，点P在y轴上的射影是M，点A 的坐标是（4，a），则当|a|＞4时，|PA|+|PM|的最小值是（ ）
A、
| ||
B、
| ||
| C、a+3 | ||
D、
|
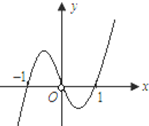已知函数y=| f′(x) |
| x |
| A、f′（1）=f′（-1）=0 |
| B、当x=-1时，函数f（x）取得极大值 |
| C、方程xf′（x）=0与f（x）=0均有三个实数根 |
| D、当x=1时，函数f（x）取得极小值 |
