题目内容
已知x,y满足约束条件
,使z=ax+y取得最小值的最优解有无数个,则a的值为( )
|
| A、-3 | B、3 | C、-1 | D、1 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式对应的平面区域,利用线性规划的知识,要使z=ax+y取最小值的最优解有无穷多个,则目标函数和其中一条直线平行,然后根据条件即可求出a的值.
解答:
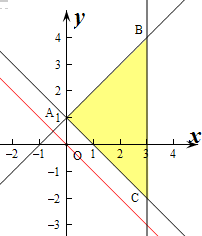 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).
由z=ax+y,得y=-ax+z,
若a=0,此时y=z,此时函数y=z只在B处取得最小值,不满足条件.
若a>0,则目标函数的斜率k=-a<0.
平移直线y=-ax+z,
由图象可知当直线y=-ax+z和直线x+y=1平行时,此时目标函数取得最小值时最优解有无数多个,
此时-a=-1,即a=1.
若a<0,则目标函数的斜率k=-a>0.
平移直线y=-ax+z,
由图象可知当直线y=-ax+z,此时目标函数只在C处取得最小值,不满足条件.
综上a=1.
故选:D.
 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).由z=ax+y,得y=-ax+z,
若a=0,此时y=z,此时函数y=z只在B处取得最小值,不满足条件.
若a>0,则目标函数的斜率k=-a<0.
平移直线y=-ax+z,
由图象可知当直线y=-ax+z和直线x+y=1平行时,此时目标函数取得最小值时最优解有无数多个,
此时-a=-1,即a=1.
若a<0,则目标函数的斜率k=-a>0.
平移直线y=-ax+z,
由图象可知当直线y=-ax+z,此时目标函数只在C处取得最小值,不满足条件.
综上a=1.
故选:D.
点评:本题主要考查线性规划的应用,利用数形结合是解决此类问题的基本方法,利用z的几何意义是解决本题的关键.注意要对a进行分类讨论.

练习册系列答案
相关题目
已知下列命题:
①“p∧q”为真,则“p∨q”为真;
②函数y=3x(x≥0)的值域为[0,+∞);
③命题“?x∈R,都有ln(x2+1)≥0”的否定为“?x0∈R,ln(x02+1)<0”.
其中真命题的个数为( )
①“p∧q”为真,则“p∨q”为真;
②函数y=3x(x≥0)的值域为[0,+∞);
③命题“?x∈R,都有ln(x2+1)≥0”的否定为“?x0∈R,ln(x02+1)<0”.
其中真命题的个数为( )
| A、0 | B、1 | C、2 | D、3 |
已知全集U=R,集合A={x|x-2>0},B={x|x2-1≤0},则(∁UA)∪B=( )
| A、{x|-1≤x≤1} |
| B、{x|-1≤x≤1或x>2} |
| C、{x|-1≤x≤2} |
| D、{x|x≤2} |
若(x-
)n的展开式中第三项系数等于6,则n等于( )
| ||
| 11 |
| A、4 | B、8 | C、12 | D、16 |
已知集合U=R,A={x|3x-x2>0},B={x|y=log2(x-2)},则A∩B为( )
| A、[2,3) | B、(2,3) |
| C、(0,2) | D、∅ |
函数y=2
-x的单调递增区间为( )
| x |
| A、[0,1] |
| B、(-∞,1] |
| C、[1,+∞) |
| D、(0,+∞) |
设曲线y=(ax-1)•ex在点A(x0,y1)处的切线为l1,曲线y=(1-x)•e-x在点A(x0,y2)处的切线为l2,若存在x0∈[0,
],使得l1⊥l2,则实数a的取值范围是( )
| 3 |
| 2 |
| A、(-∞,1] | ||
B、[
| ||
C、(1,
| ||
D、[1,
|