题目内容
若曲线y=x2+ax+b在点（0，b）处的切线方程是x-y+1=0，则a-b= ．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：根据导数的几何意义求出函数y在x=0处的导数，从而求出切线的斜率，建立等量关系求出a，再根据点（0，b）在切线x-y+1=0上求出b即可．
解答：
解：∵曲线y=x2+ax+b在点（0，b）处的切线方程是x-y+1=0，
∴切线的斜率为1，切点为（0，1），可得b=1．
又∵y′=2x+a，∴2×0+a=1，解得a=1．
∴a-b=0．
故答案为：0．
∴切线的斜率为1，切点为（0，1），可得b=1．
又∵y′=2x+a，∴2×0+a=1，解得a=1．
∴a-b=0．
故答案为：0．
点评：熟练掌握导数的几何意义和切线方程是解题的关键．
练习册系列答案
相关题目
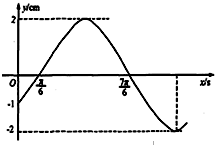如图是某简谐运动的一段图象，其函数模型是f（x）=Asin（ωx+φ）（x≥0），其中A＞0，ω＞0，-
已知函数f（x）=已知x，y满足约束条件
，使z=ax+y取得最小值的最优解有无数个，则a的值为（ ）
|
| A、-3 | B、3 | C、-1 | D、1 |