Question

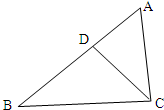在△ABC中，∠A=60°，BC=

10

，D是AB边上的一点，CD=

2

，△CBD的面积为1．
（1）求BD的长；
（2）求sin∠ACD的值．

Answer 1

考点：余弦定理,正弦定理

专题：解三角形

分析：（1）由△CBD的面积为1，求得sin∠BCD的值，可得cos∠BCD 的值，再由余弦定理求得BD的值．
（2）在△BCD中，由余弦定理 cos∠BDC的值，可得∠BDC的值，从而求得∠ACD=∠BDC-∠A=75°，再利用两角和的正弦公式，求得sin∠BDC=sin（45°+30°）的值．

解答： 解：（1）∵△CBD的面积为

1

2

CB•CD•sin∠BCD=

1

2

•

10

•

2

sin∠BCD=1，
求得sin∠BCD=

5

5

，∴cos∠BCD=

2 5

5

．
由余弦定理可得BD²=CB²+CD²-2CB•CD•cos∠BCD=10+2-2•

10

•

2

•

2 5

5

=4
故BD=2．
（2）在△BCD中，由余弦定理 cos∠BDC=

BD2+BC2-BC2

2BD•BC

=-

2

2

，∴∠BDC=135°．
∴∠ACD=∠BDC-∠A=135°-60°=75°，
∴sin∠BDC=sin（45°+30°）=sin45°cos30°+cos45°sin30°=

2

2

×

3

2

+

2

2

×

1

2

=

6 + 2

4

．

点评：本题主要考查正弦定理和余弦定理的应用，两角和的正弦公式，属于基础题．