题目内容
若集合M={1,2},N={-1,1,3},则M∩N等于 .
考点:交集及其运算
专题:集合
分析:由M与N,求出两集合的交集即可.
解答:
解:∵M={1,2},N={-1,1,3},
∴M∩N={1}.
故答案为:{1}
∴M∩N={1}.
故答案为:{1}
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
函数f(x)=
+lg(x+1)的定义域为( )
| 3x2 | ||
|
| A、(-1,1) |
| B、(-1,+∞) |
| C、(1,+∞) |
| D、(-∞,1) |
设全集U=R,集合A={x|x>1},B={x|x2-2x-3≥0},则A∩(∁UB)=( )
| A、{x|x≤-1} |
| B、{x|x≤1} |
| C、{x|-1<x≤1} |
| D、{x|1<x<3} |
如果x∈(-
,0)时总有k(x+
)>cosx成立,则实数k的取值范围是( )
| π |
| 2 |
| π |
| 2 |
| A、(1,+∞) | ||
| B、[1,+∞) | ||
C、(
| ||
D、[
|
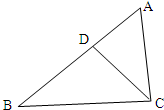 在△ABC中,∠A=60°,BC=
在△ABC中,∠A=60°,BC=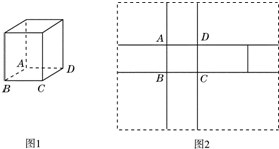 图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是
图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是