题目内容
某公司的男女职工的人数之比为4:1,用分层抽样的方法从该公司的所有职工中抽取一个容量为10的样本.已知女职工中甲、乙都被抽到的概率为
,则公司的职工总人数为 .
| 1 |
| 28 |
考点:古典概型及其概率计算公式,分层抽样方法
专题:概率与统计
分析:由题意设女职工有n人,则男职工有4n人,由题意可得
=
,解得n值可得答案.
| 1 | ||
|
| 1 |
| 28 |
解答:
解:由题意设女职工有n人,则男职工有4n人
∵女职工中甲、乙都被抽到的概率为
,
∴
=
,整理可得n2-n-56=0,
解得n=-7(舍去),n=8,
∴公司的职工总人数为(4+1)×8=40
故答案为:40
∵女职工中甲、乙都被抽到的概率为
| 1 |
| 28 |
∴
| 1 | ||
|
| 1 |
| 28 |
解得n=-7(舍去),n=8,
∴公司的职工总人数为(4+1)×8=40
故答案为:40
点评:本题考查古典概型及其概率公式,涉及分层抽样,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
焦点为(0,6)且过点(2,5)双曲线方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设数列{an}是公差d<0的等差数列,Sn为其前n项和,若S6=5a1+10d,则Sn取最大值时,n=( )
| A、5 | B、6 | C、5或6 | D、6或7 |
已知f(x)是定义在R上的奇函数,当x≥0时f(x)=ex+m(m为常数),则f(-ln5)的值为( )
| A、-4 | B、4 | C、-6 | D、6 |
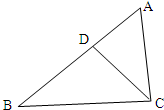 在△ABC中,∠A=60°,BC=
在△ABC中,∠A=60°,BC=