题目内容
Sn是等差数列{an}的前n项和,S6>S7>S5,则下列命题正确的是 .
①d<0; ②S11>0; ③S12<0; ④数列的最大项为S11.
①d<0; ②S11>0; ③S12<0; ④数列的最大项为S11.
考点:等差数列的性质
专题:计算题
分析:依题意,可求得a6>0,a7<0,a6+a7>0,利用等差数列的概念及性质对①②③④四个选项逐一判断即可.
解答:
解:∵{an} 是等差数列,Sn是其前n项和,且S6>S7>S5,
∴a6>0,a7<0,a6+a7>0;
∴d=a7-a6<0,故①正确;
S11=
=11a6>0,故②正确;
同理可得,S12=6(a6+a7)>0,故③错误;
由以上分析可知,公差d<0,a6>0,a7<0,故数列{Sn}中的最大项为S6,非S11,故④错误;
综上所述,正确的命题是①②.
故答案为①②.
∴a6>0,a7<0,a6+a7>0;
∴d=a7-a6<0,故①正确;
S11=
| 11(a1+a11) |
| 2 |
同理可得,S12=6(a6+a7)>0,故③错误;
由以上分析可知,公差d<0,a6>0,a7<0,故数列{Sn}中的最大项为S6,非S11,故④错误;
综上所述,正确的命题是①②.
故答案为①②.
点评:本题考查等差数列的概念及性质应用,突出考查数列{Sn}中的最值问题,考查化归思想与分析、运算能力,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
已知函数f(x)是定义在R上的偶函数,且在[0,+∞)上为增函数,若f(log2x)>f(1),则x的取值范围是( )
| A、(2,+∞) | ||
B、(
| ||
C、(0,
| ||
| D、(0,1)∪(2,+∞) |
已知f(x)是定义在R上的奇函数,当x≥0时f(x)=ex+m(m为常数),则f(-ln5)的值为( )
| A、-4 | B、4 | C、-6 | D、6 |
设a=70.3,b=log70.3,c=0.37,则a,b,c的大小关系是( )
| A、a<b<c |
| B、b<c<a |
| C、c<a<b |
| D、c<b<a |
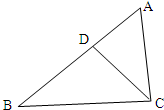 在△ABC中,∠A=60°,BC=
在△ABC中,∠A=60°,BC=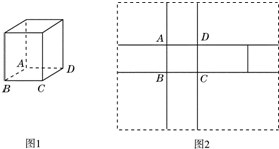 图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是
图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是