题目内容
已知数列{an}满足log3an+1=log3an-1,且a2+a4+a8=9,则log
(a6+a8+a12)= .
| 1 |
| 3 |
考点:等差数列的性质,对数的运算性质
专题:计算题,等差数列与等比数列
分析:先由数列{an}满足log3an+1=log3an-1探讨数列,得到数列是以
为公比的等比数列,再由a2+a4+a6=a2(1+q2+q4),a6+a8+a12=a6(1+q2+q4)=a2q4(1+q2+q4)求解.
| 1 |
| 3 |
解答:
解:∵log3an-1=log3an+1
∴an+1=
an
∴数列{an}是以
为公比的等比数列,
∴a2+a4+a6=a2(1+q2+q4)=9
∴a6+a8+a12=a6(1+q2+q4)=a2q4(1+q2+q4)=9×
=
,
∴log
(a6+a8+a12)=2
故答案为:2.
∴an+1=
| 1 |
| 3 |
∴数列{an}是以
| 1 |
| 3 |
∴a2+a4+a6=a2(1+q2+q4)=9
∴a6+a8+a12=a6(1+q2+q4)=a2q4(1+q2+q4)=9×
| 1 |
| 81 |
| 1 |
| 9 |
∴log
| 1 |
| 3 |
故答案为:2.
点评:本题考查了等比数列的定义及其性质、对数的运算性质,考查了计算能力,属于基础题.

练习册系列答案
相关题目
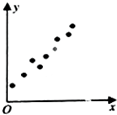 已知变量x与y呈相关关系,且由观测数据得到的样本数据散点图如图所示,则由该观测数据算得的回归方程可能是( )
已知变量x与y呈相关关系,且由观测数据得到的样本数据散点图如图所示,则由该观测数据算得的回归方程可能是( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)是定义在R上的偶函数,且在[0,+∞)上为增函数,若f(log2x)>f(1),则x的取值范围是( )
| A、(2,+∞) | ||
B、(
| ||
C、(0,
| ||
| D、(0,1)∪(2,+∞) |
下列函数中,在其定义域内为增函数的是( )
| A、f(x)=x2 | ||
B、f(x)=-
| ||
| C、f(x)=|x| | ||
| D、f(x)=x3 |
设a=70.3,b=log70.3,c=0.37,则a,b,c的大小关系是( )
| A、a<b<c |
| B、b<c<a |
| C、c<a<b |
| D、c<b<a |
设全集U=R,集合A={x|x>1},B={x|x2-2x-3≥0},则A∩(∁UB)=( )
| A、{x|x≤-1} |
| B、{x|x≤1} |
| C、{x|-1<x≤1} |
| D、{x|1<x<3} |
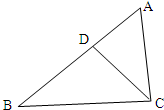 在△ABC中,∠A=60°,BC=
在△ABC中,∠A=60°,BC=