题目内容
若2-m与m-3同号,则实数m的取值范围是 .
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:又2-m与m-3同号,得出(2-m)(m-3)>0,求出解集即可.
解答:
解:当2-m与m-3同号时,
(2-m)(m-3)>0,
即(m-2)(m-3)<0,
解得2<m<3;
∴实数m的取值范围是(2,-3).
故答案为:(2,-3).
(2-m)(m-3)>0,
即(m-2)(m-3)<0,
解得2<m<3;
∴实数m的取值范围是(2,-3).
故答案为:(2,-3).
点评:本题考查了一元二次不等式的解法与应用问题,是基础题目.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
椭圆x2+
=1的一个焦点是(0,
),那么k=( )
| y2 |
| k |
| 5 |
| A、-6 | ||
| B、6 | ||
C、
| ||
D、1-
|
函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x2+1,则f(-1)等于( )
| A、1 | B、-1 | C、2 | D、-2 |
设数列{an}是等比数列,函数y=x2-x-2的两个零点是a2,a3,则a1a4=( )
| A、2 | B、1 | C、-1 | D、-2 |
双曲线
-
=-5的一条渐近线方程是( )
| x2 |
| 4 |
| y2 |
| 9 |
| A、2x-3y=0 |
| B、3x+2y=0 |
| C、9x-4y=0 |
| D、4x-9y=0 |
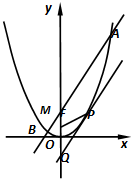 如图,设抛物线C:x2=4y的焦点为F,P(x0,y0)为抛物线上的任一点(其中x0≠0),过P点的切线交y轴于Q点.
如图,设抛物线C:x2=4y的焦点为F,P(x0,y0)为抛物线上的任一点(其中x0≠0),过P点的切线交y轴于Q点.