题目内容
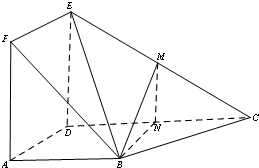
 如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,ED=2
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,ED=2| 2 |
(1)求证:平面BMN∥平面ADEF;
(2)求证:平面BCE⊥平面BDE;
(3)求点D到平面BEC的距离.
考点:平面与平面垂直的判定,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)由MN∥ED,得MN∥平面ADEF,得平面BMN∥平面ADEF;
(2)由题意得ED⊥BC,得BC⊥BD,从而得BC⊥平面BDE.进而平面BCE⊥平面BDE,
(3)设点D到平面BEC的距离为h,转化为VD-BEC=VE-BCD,从而求出h的值.
(2)由题意得ED⊥BC,得BC⊥BD,从而得BC⊥平面BDE.进而平面BCE⊥平面BDE,
(3)设点D到平面BEC的距离为h,转化为VD-BEC=VE-BCD,从而求出h的值.
解答:
 (1)证明:在△EDC中,M,N分别为EC,DC的中点,
(1)证明:在△EDC中,M,N分别为EC,DC的中点,
所以MN∥ED,又DE?平面ADEF,且MN?平面ADEF,
所以MN∥平面ADEF;
因为N为CD中点,AB∥CD,AB=2,CD=4,
所以四边形ABND为平行四边形,所以BN∥DA,
又DA?平面ADEF,且BN?平面ADEF,
所以BN∥平面ADEF,
∵BN∩MN=N,EN,MN?面BMN,
∴平面BMN∥平面ADEF;
(2)证明:在矩形ADEF中,ED⊥AD.又
因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD.所以ED⊥BC.
在直角梯形ABCD中,AB=AD=2,CD=4,可得BC=2
.
在△BCD中,BD=BC=2
,CD=4,因为BD2+BC2=CD2,
所以BC⊥BD.
因为BD∩DE=D,所以BC⊥平面BDE.
因为BC?面BCE,所以平面BCE⊥平面BDE,
(3)设点D到平面BEC的距离为h,
则VD-BEC=VE-BCD,
求得h=2.
 (1)证明:在△EDC中,M,N分别为EC,DC的中点,
(1)证明:在△EDC中,M,N分别为EC,DC的中点,所以MN∥ED,又DE?平面ADEF,且MN?平面ADEF,
所以MN∥平面ADEF;
因为N为CD中点,AB∥CD,AB=2,CD=4,
所以四边形ABND为平行四边形,所以BN∥DA,
又DA?平面ADEF,且BN?平面ADEF,
所以BN∥平面ADEF,
∵BN∩MN=N,EN,MN?面BMN,
∴平面BMN∥平面ADEF;
(2)证明:在矩形ADEF中,ED⊥AD.又
因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD.所以ED⊥BC.
在直角梯形ABCD中,AB=AD=2,CD=4,可得BC=2
| 2 |
在△BCD中,BD=BC=2
| 2 |
所以BC⊥BD.
因为BD∩DE=D,所以BC⊥平面BDE.
因为BC?面BCE,所以平面BCE⊥平面BDE,
(3)设点D到平面BEC的距离为h,
则VD-BEC=VE-BCD,
求得h=2.
点评:本题考查了面面平行,面面垂直的判定,考查转化思想,是一道综合题.

练习册系列答案
相关题目
观察:52-1=24,72-1=48,112-1=120,132-1=168,…所得的结果都是24的倍数,由此推测可有( )
| A、其中包含等式:152-1=224 |
| B、一般式是:(2n+3)2-1=4(n+1)(n+2) |
| C、其中包含等式1012-1=10200 |
| D、24的倍数加1必是某一质数的完全平方 |
△ABC中,已知b=15,c=30,C=123°,则此三角形的解的情况是( )
| A、一解 | B、二解 |
| C、无解 | D、无法确定 |
若|
|=6,|
|=4,
•
=-12
,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、120° | B、150° |
| C、135° | D、45° |
一个正方体的顶点都在球面上,它的棱长为2cm,则球的表面积是( )
| A、8πcm2 |
| B、12πcm2 |
| C、16πcm2 |
| D、20πcm2 |