题目内容
△ABC中，已知b=15，c=30，C=123°，则此三角形的解的情况是（ ）
| A、一解 | B、二解 |
| C、无解 | D、无法确定 |
考点：正弦定理
专题：解三角形
分析：利用正弦定理列出关系式，把b，c，sinC的值代入表示出sinB，根据sinB的范围，以及三角形边角关系判断即可得到结果．
解答：
解：∵△ABC中，b=15，c=30，C=123°，
∴由正弦定理
=
得：sinB=
=
=
sin123°＜
，
∴此三角形有解，
∵b＜c，∴B＜C，
则此三角形只有一解，B为锐角．
故选：A．
∴由正弦定理
| b |
| sinB |
| c |
| sinC |
| bsinC |
| c |
| 15sin123° |
| 30 |
| 1 |
| 2 |
| 1 |
| 2 |
∴此三角形有解，
∵b＜c，∴B＜C，
则此三角形只有一解，B为锐角．
故选：A．
点评：此题考查了正弦定理，熟练掌握正弦定理是解本题的关键．
练习册系列答案
小学课时特训系列答案
相关题目
| cos85°+sin25°cos30° |
| cos25° |
A、-
| ||||
B、
| ||||
C、
| ||||
| D、1 |
设 a＞b，则下列不等式中恒成立的是（ ）
| A、a2＞b2 | ||||
B、
| ||||
| C、lg（a-b）＞0 | ||||
| D、2a＞2b |
设集合M={x|f（x）=0}，N={x|g（x）=0}，则集合P={x|f（x）•g（x）=0}一定（ ）
| A、等于M∩N |
| B、等于M∪N |
| C、等于 M或N |
| D、以上都不对 |
用数字1、2、3、4、5可组成没有重复数字的三位数共有（ ）
| A、10个 | B、15个 |
| C、60个 | D、125个 |
下列三视图表示的几何体是（ ）
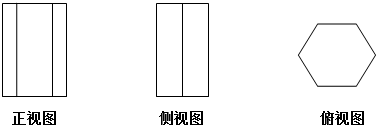
| A、正六棱柱 | B、正六棱锥 |
| C、正六棱台 | D、正六边形 |
如图，矩形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AB∥CD，AB=AD=2，CD=4，ED=2