题目内容
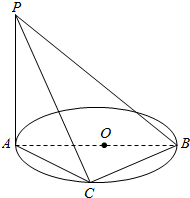 如图,AB是圆O的直径,AB=5,PA垂直于圆O所在的平面,C是圆周上一点,AC=PA=4,求:
如图,AB是圆O的直径,AB=5,PA垂直于圆O所在的平面,C是圆周上一点,AC=PA=4,求:(1)直线PA与BC所成的角;
(2)二面角P-BC-A的大小;
(3)三棱锥A-PBC的体积.
考点:用空间向量求平面间的夹角,棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题:空间角
分析:(1)判定PA⊥BC,即可得到直线PA与BC所成的角;
(2)求出二面角P-BC-A的平面角,即可求出二面角的大小;
(3)根据三棱锥A-PBC的体积公式,即可得到结论.
(2)求出二面角P-BC-A的平面角,即可求出二面角的大小;
(3)根据三棱锥A-PBC的体积公式,即可得到结论.
解答:
解:(1)由PA⊥平面ABC,BC?平面ABC,
得PA⊥BC.
∴直线PA与BC所成的角为90°.
(2)由AB是圆的直径,得AC⊥BC,
又PA∩AC=A,PA?平面PAC,AC?平面PAC,
∴BC⊥平面PAC.则BC⊥PC.
即∠PCA是二面角P-BC-A的平面角,
∵AC=PA=4,
∴tan∠PCA=
=1,即∠PCA=
.
(3)∵AB=5,AC=4,
∴BC=3,即△ABC的面积S=
×3×4=6,
则∵三棱锥A-PBC的体积等于三棱锥P-ABC的体积,
∴V=
×S△ABC×PA=
×6×4=8,
故三棱锥的体积为8.
得PA⊥BC.
∴直线PA与BC所成的角为90°.
(2)由AB是圆的直径,得AC⊥BC,
又PA∩AC=A,PA?平面PAC,AC?平面PAC,
∴BC⊥平面PAC.则BC⊥PC.
即∠PCA是二面角P-BC-A的平面角,
∵AC=PA=4,
∴tan∠PCA=
| PA |
| AC |
| π |
| 4 |
(3)∵AB=5,AC=4,
∴BC=3,即△ABC的面积S=
| 1 |
| 2 |
则∵三棱锥A-PBC的体积等于三棱锥P-ABC的体积,
∴V=
| 1 |
| 3 |
| 1 |
| 3 |
故三棱锥的体积为8.
点评:本题考查的知识点是二面角的求解,棱锥的体积,其中熟练掌握空间线线垂直,线面垂直的判定是解决本题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
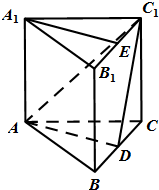 如图,正三棱柱ABC-A1B1C1的侧棱为2,底面是边长为2的等边三角形,D,E分别是线段BC,B1C1的中点.
如图,正三棱柱ABC-A1B1C1的侧棱为2,底面是边长为2的等边三角形,D,E分别是线段BC,B1C1的中点.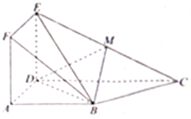 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AD=
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AD=